Đề khảo sát Toán 12 lần 1 năm 2025 – 2026 trường THPT Lê Quý Đôn – Hà Nội (mã 1281)
Thí sinh đọc kỹ đề trước khi làm bài
Cài đặt đề thi
Vui lòng cài đặt đề thi trước khi làm bài
Câu 1
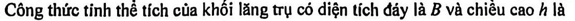
Câu 2
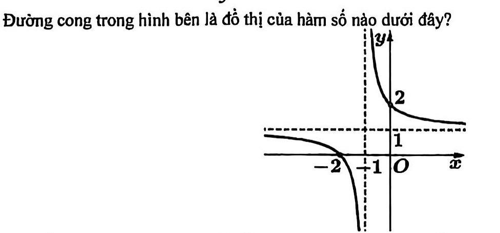

Câu 3
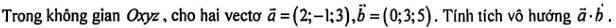
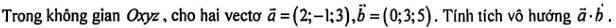
Câu 4
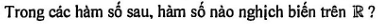
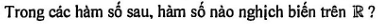
Câu 5
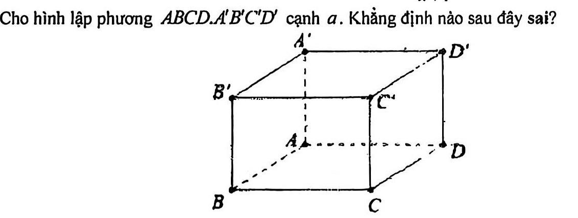

Câu 6
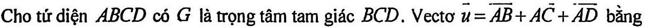
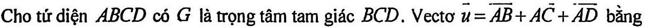
Câu 7
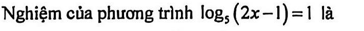
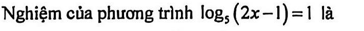
Câu 8
Cho hàm số $y= f(x)$ liên tục trên đoạn $[-1;3] và có đồ thị như hình vẽ bên. 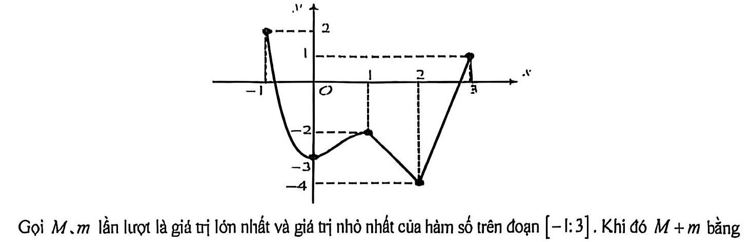

Câu 9
Cho cấp số nhân $(u_n)$ có số hạng đầu $u_1 = 7$ và công bội $q = 3$. Khi đó số hạng thứ hai của cấp số nhân đã cho là:
Câu 10
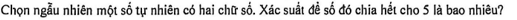
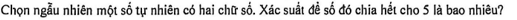
Câu 11
$Quãng đường đi bộ mỗi ngày (đơn vị: km) của bạn Dũng trong 20 ngày gần nhất được thống kê lại ở bảng sau:$ 

Câu 12
Cho hàm số $f(x)$ có đạo hàm $f'(x) = x(x-1)(x-2)^2, \forall x \in \mathbb{R}$. Số điểm cực trị của hàm số đã cho là:
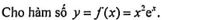
Câu 13
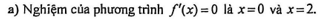
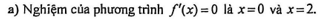
Câu 14


Câu 15
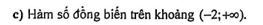
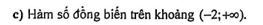
Câu 16
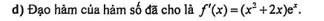
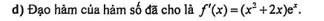
$Cho hàm số y= f(x) có đạo hàm trên R và hàm số y= f'(x) là hàm só bậc ba có đồ thị là đường cong trong hình vẽ sau:$ 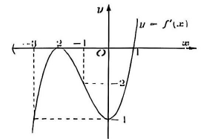

Câu 17
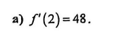
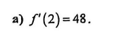
Câu 18
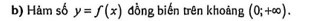
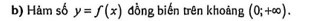
Câu 19
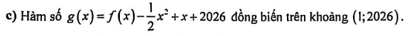
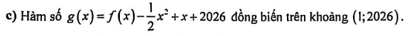
Câu 20


Một chiếc máy bay thương mại đang bay trên bầu trời theo một đường thẳng từ $D$ đến $E$ có hình chiếu trên mặt đất là đoạn $CB$. Tại vị trí $D$ thì máy bay bay cách mặt đất $9000$ m, tại vị trí $E$ thì máy bay cách mặt đất $12000$ m. Một radar được đặt trên mặt đất tại vị trí $O$ cách $C$ khoảng $20000$ m, cách $B$ khoảng $16000$ m và $\widehat{BOC} = 90^\circ$, phạm vi theo dõi của radar là $20$ km. Xét hệ trục tọa độ $Oxyz$ (đơn vị trên mỗi trục là $1000$ m) với $O$ là vị trí đặt radar, $B$ thuộc tia $Oy$, $C$ thuộc tia $Ox$. 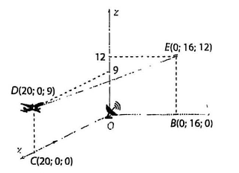

Câu 21
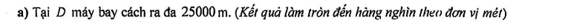
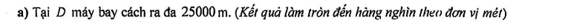
Câu 22
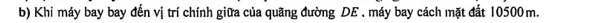
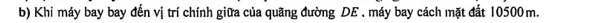
Câu 23
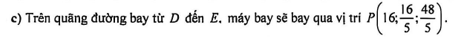
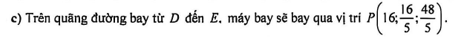
Câu 24
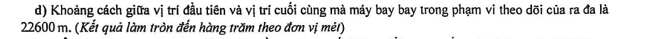
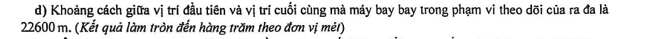
Ông Minh vay ngân hàng $100$ triệu đồng với lãi suất không đổi trong suốt quá trình vay là $1\%$/tháng. Ông Minh hoàn nợ cho ngân hàng theo cách:Sau đúng một tháng kể từ ngày vay, ông bắt đầu hoàn nợ.Hai lần hoàn nợ liên tiếp cách nhau đúng một tháng, số tiền hoàn nợ ở mỗi tháng là như nhau. Biết rằng mỗi tháng ngân hàng chỉ tính lãi trên số dư nợ thực tế của tháng đó. 

Câu 25
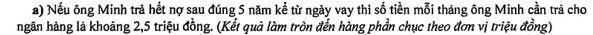
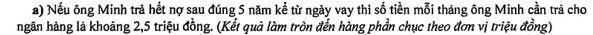
Câu 26
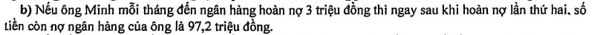
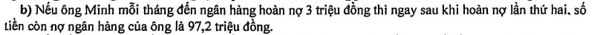
Câu 27


Câu 28


Câu 29
Một bác tài xế thống kê lại độ dài quãng đường (đơn vị: km) bác đã lái xe mỗi ngày trong một tháng ở bảng sau: 

Câu 30
Cho hình lập phương $ABCD.A'B'C'D'$ có cạnh bằng $20$ cm. Giả sử hai chú kiến vàng và đen xuất phát cùng một lúc tại các vị trí $A$ và $D$, kiến vàng đi thẳng từ $A$ đến $D'$ với vận tốc $2$ cm/s và kiến đen đi thẳng từ $D$ đến $B$ với vận tốc $3$ cm/s. Hỏi khoảng cách ngắn nhất giữa hai chú kiến là bao nhiêu cm. (Kết quả làm tròn đến hàng phần chục). 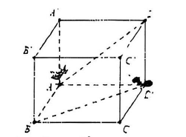

Câu 31
Một doanh nghiệp kinh doanh một loại sản phẩm $T$ được sản xuất trong nước. Qua nghiên cứu thấy rằng nếu chi phí sản xuất mỗi sản phẩm $T$ là $x$ (USD) thì số sản phẩm $T$ các nhà máy sản xuất sẽ là $R(x) = 30x - 200$ và số sản phẩm $T$ mà doanh nghiệp bán được trên thị trường trong nước sẽ là $Q(x) = 3000 - 10x$. Số sản phẩm còn dư doanh nghiệp xuất khẩu ra thị trường quốc tế với giá bán mỗi sản phẩm ổn định trên thị trường quốc tế là $150$ (USD). Nhà nước đánh thuế trên mỗi sản phẩm xuất khẩu là $a$ (USD) và luôn đảm bảo tỉ lệ giữa lợi nhuận từ việc xuất khẩu của doanh nghiệp và thuế thu được của nhà nước tương ứng là $4:1$. Hãy tìm giá trị của $a$ biết lợi nhuận mà doanh nghiệp thu được từ việc xuất khẩu là nhiều nhất.
Câu 32
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh bằng $1$, cạnh bên $SA$ vuông góc với đáy. Góc giữa đường thẳng $SC$ và mặt phẳng $(ABCD)$ bằng $45^\circ$. Tính khoảng cách giữa hai đường thẳng $SC$ và $BD$.
Câu 33
Một bể bơi ban đầu có dạng hình hộp chữ nhật $ABCD.A'B'C'D'$. Sau đó người ta làm lại mặt đáy như hình vẽ. Biết rằng $A'B'MN$ và $MNEF$ là các hình chữ nhật, $(MNFE) // (A'B'C'D')$, $AB = 10$ m, $AD = 30$ m, $AA' = 2$ m, $MF = 20$ m, $DE = 1,7$ m. Tính tỉ số thể tích của bể sau khi làm lại mặt đáy với thể tích của bể lúc ban đầu. (Kết quả làm tròn đến hàng phần trăm)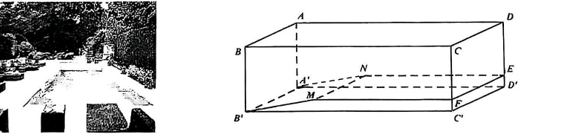

Câu 34
Hộp A có $5$ bi đỏ và $3$ bi vàng, hộp B có $2$ bi đỏ và $2$ bi vàng, hộp C có $2$ bi đỏ và $2$ bi vàng. Lấy ngẫu nhiên $1$ bi từ hộp A bỏ sang hộp B, rồi lấy ngẫu nhiên $2$ bi từ hộp B bỏ sang hộp C, sau cùng lấy ngẫu nhiên $3$ bi từ hộp C. Xác suất để lấy được $3$ bi đỏ từ hộp C là $\frac{a}{b}$ ($\frac{a}{b}$ là phân số tối giản, $a; b \in \mathbb{N}^*$). Tính $a - b$. 


