Megaedu.AI - Đề thi thử giữa học kỳ 1 môn Toán lớp 11 online

Câu 1

Hàm số $y = \sin 3x.\cos x$ là một hàm số tuần hoàn có chu kì là

A.

$\pi$

B.

$\dfrac{\pi }{4}$

C.

$\dfrac{\pi }{3}$

D.

$\dfrac{\pi }{2}$

Lời giải :

Ta có: $y = \sin 3x.\cos x = \dfrac{1}{2}\left( {\sin 4x + \sin 2x} \right)$

Hàm số $y = \sin 4x$ tuần hoàn với chu kì ${T_1} = \frac{{2\pi }}{4} = \frac{\pi }{2}$

Hàm số $y = \sin 2x$ tuần hoàn với chu kì ${T_2} = \frac{{2\pi }}{2} = \pi$

Vậy hàm số $y = \frac{1}{2}\left( {\sin 4x + \sin 2x} \right)$ tuần hoàn với chu kì $T = BCNN\left( {\frac{\pi }{2};\pi } \right) = \pi$

Câu 2

Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số $y = {\sin ^4}x - 2{\cos ^2}x + 1$

A.

$M = 2, m = -2$

B.

$M = 1, m = 0$

C.

$M = 4, m = -1$

D.

$M = 2, m = -1$

Lời giải :

Ta có:

$y = {\sin ^4}x - 2{\cos ^2}x + 1$ $= {\sin ^4}x - 2\left( {1 - {{\sin }^2}x} \right) + 1$

$= {\sin ^4}x + 2{\sin ^2}x - 1$ $= {\left( {{{\sin }^2}x + 1} \right)^2} - 2$

$\begin{array}{l}0 \le {\sin ^2}x \le 1\\\Rightarrow 1 \le {\sin ^2}x + 1 \le 2\\\Rightarrow 1 \le {\left( {{{\sin }^2}x + 1} \right)^2} \le 4\\\Rightarrow - 1 \le {\left( {{{\sin }^2}x + 1} \right)^2} - 2 \le 2\end{array}$

$\Rightarrow - 1 \le y \le 2$

Câu 3

Tập xác định của hàm số $y = \sqrt {1 - \cos 2017x}$ là

A.

$D = \mathbb{R}\backslash \left\{ {k\pi \left| {k \in \mathbb{Z}} \right.} \right\}$

B.

$D = \mathbb{R}$

C.

$D = \mathbb{R}\backslash \left\{ {\dfrac{\pi }{4} + k\pi ;\,\dfrac{\pi }{2} + k\pi \left| {k \in \mathbb{Z}} \right.} \right\}$

D.

$D = \mathbb{R}\backslash \left\{ {\dfrac{\pi }{2} + k2\pi \left| {k \in \mathbb{Z}} \right.} \right\}$

Lời giải :

Điều kiện xác định: $1 - \cos 2017x \ge 0 \Leftrightarrow \cos 2017x \le 1$ luôn đúng với mọi $x \in \mathbb{R}$

Vậy TXĐ: D=R.

Câu 4

Tìm chu kì T của hàm số $y = \cot 3x + \tan x$ là

A.

$\pi$

B.

$3\pi$

C.

$\dfrac{\pi }{3}$

D.

$4\pi$

Lời giải :

Chu kì của hàm số $y = \cot 3x + \tan x$ là $T = \pi$

Câu 5

Cho hàm số $f\left( x \right) = \left| x \right|\sin x.$ Phát biểu nào sau đây là đúng về hàm số đã cho?

A. Hàm số đã cho có tập xác định

$D = \mathbb{R}\backslash \left\{ 0 \right\}.$

B. Đồ thị hàm số đã cho có tâm đối xứng.

C. Đồ thị hàm số đã cho có trục đối xứng.

D. Hàm số có tập giá trị là

$\left[ { - 1;\,1} \right].$

Lời giải :

Hàm số $y = \left| x \right|\sin x$ có:

$\begin{array}{l}y\left( { - x} \right) = \left| { - x} \right|\sin \left( { - x} \right)\\ = - \left| x \right|\sin x = - y\left( x \right)\end{array}$

Nên là hàm số lẻ.

Do đó đồ thị hàm số nhận gốc O làm tâm đối xứng.

Câu 6

Trong các phương trình sau đây,phương trình nào có tập nghiệm là $x = - \dfrac{\pi }{3} + k2\pi$ và $x = \dfrac{{4\pi }}{3} + k2\pi ,\,\,\,(k \in \mathbb{Z})$

A.

$\sin \,x = \dfrac{2}{{\sqrt 2 }}$

B.

$\sin \,x = \dfrac{1}{{\sqrt 2 }}$

C.

$\sin \,x = - \dfrac{{\sqrt 3 }}{2}$

D.

$\sin \,x = \dfrac{{\sqrt 2 }}{{\sqrt 3 }}$

Lời giải :

Ta có:

$\sin x = - \dfrac{{\sqrt 3 }}{2}$ $\Leftrightarrow \left[ \begin{array}{l}x = - \dfrac{\pi }{3} + k2\pi \\x = \dfrac{{4\pi }}{3} + k2\pi \end{array} \right.\;\left( {k \in \mathbb{Z}} \right)$

Câu 7

Phương trình $\tan \left( {3x - {{15}^0}} \right) = \sqrt 3$ có các nghiệm là:

A.

$x = {60^0} + k{180^0}$

B.

$x = {75^0} + k{180^0}$

C.

$x = {75^0} + k{60^0}$

D.

$x = {25^0} + k{60^0}$

Lời giải :

Ta có: $\tan \left( {3x - {{15}^ \circ }} \right) = \sqrt 3\Leftrightarrow \tan \left( {3x - {{15}^ \circ }} \right) = \tan {60^ \circ }$

$\Leftrightarrow 3x - {15^ \circ } = {60^ \circ } + k{180^ \circ }$

$\Leftrightarrow x = {25^ \circ } + k{60^ \circ }\;\left( {k \in \mathbb{Z}} \right)$

Câu 8

Nghiệm âm lớn nhất của phương trình $\dfrac{{\sqrt 3 }}{{{{\sin }^2}\,x}} = 3\cot \, + \,\sqrt 3$ là:

A.

$- \dfrac{\pi }{2}$

B.

$- \dfrac{{5\pi }}{6}$

C.

$- \dfrac{\pi }{6}$

D.

$- \dfrac{{2\pi }}{3}$

Lời giải :

Điều kiện: $\sin x \ne 0 \Leftrightarrow x \pm k\pi \,\left( {k \in \mathbb{Z}} \right)$

Ta có: $\dfrac{{\sqrt 3 }}{{{{\sin }^2}x}} = 3\cot x + \sqrt 3$

$\begin{array}{l}\Leftrightarrow \sqrt 3 \left( {1 + {{\cot }^2}x} \right) = 3\cot x + \sqrt 3 \\\Leftrightarrow \sqrt 3 {\cot ^2}x - 3\cot x = 0\\\Leftrightarrow \cot x\left( {\sqrt 3 \cot x - 3} \right) = 0\\\Leftrightarrow \left[ \begin{array}{l}\cot x = 0\\\cot x = \sqrt 3\end{array} \right.\end{array}$

$\Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{2} + k\pi \\x = \dfrac{\pi }{6} + k\pi \end{array} \right.\;\left( {k \in \mathbb{Z}} \right)$

Nghiệm âm lớn nhất là $- \dfrac{\pi }{2}$

Câu 9

Phương trình $sin x + cos x – 1 = 2sin xcos x$ có bao nhiêu nghiệm trên $\left[ {0;\,2\pi } \right]$ ?

A. 2

B. 3

C. 4

D. 6

Lời giải :

Ta có: $\sin x + \cos x - 1 = 2\sin x\cos x$

$\begin{array}{l}\Leftrightarrow \sin x + \cos x = 1 + 2\sin x\cos x\\\Leftrightarrow \sin x + \cos x = {\sin ^2}x + {\cos ^2}x + 2\sin x\cos x\\\Leftrightarrow \sin x + \cos x = {\left( {\sin x + \cos x} \right)^2}\end{array}$

$\Leftrightarrow \left( {\sin x + \cos x} \right)\left( {1 - \sin x - \cos x} \right) = 0$

$\begin{array}{l}\Leftrightarrow \left[ \begin{array}{l}\sin x + \cos x = 0\\1 - \sin x - \cos x = 0\end{array} \right.\\\Leftrightarrow \left[ \begin{array}{l}\sin x = - \cos x\\\sin x + \cos x = 1\end{array} \right.\end{array}$

$\Leftrightarrow \left[ \begin{array}{l}\tan x = - 1\\\sin \left( {x + \dfrac{\pi }{4}} \right) = \dfrac{1}{{\sqrt 2 }}\end{array} \right.$ $\Leftrightarrow \left[ \begin{array}{l}x = - \dfrac{\pi }{4} + k\pi \\x = k2\pi \\x = \dfrac{\pi }{2} + k2\pi \end{array} \right.\,\left( {k \in \mathbb{Z}} \right)$

Các nghiệm trên $\left[ {0;2\pi } \right]$ là $\left\{ {\dfrac{{3\pi }}{4};0;2\pi ;\dfrac{\pi }{2}} \right\}$

Câu 10

Phương trình $\sin (x + {10^0}) = \dfrac{1}{2}\,\,({0^0} < x < {180^0})$ có nghiệm là:

A.

$x = {30^0}$ và

$x = {150^0}$

B.

$x = {20^0}$ và

$x = {140^0}$

C.

$x = {40^0}$ và

$x = {160^0}$

D.

$x = {30^0}$ và

$x = {140^0}$

Lời giải :

Ta có: $\sin (x + {10^0}) = \dfrac{1}{2} \Leftrightarrow \sin (x + {10^0}) = \sin {30^ \circ }$

$\Leftrightarrow \left[ \begin{array}{l}x + {10^ \circ } = {30^ \circ } + k{360^ \circ }\\x + {10^ \circ } = {150^ \circ } + k{360^ \circ }\end{array} \right.$ $\Leftrightarrow \left[ \begin{array}{l}x = {20^ \circ } + k{360^ \circ }\\x = {140^ \circ } + k{360^ \circ }\end{array} \right.$

${0^0} < x < {180^0}$ $\Rightarrow {x_1} = {20^0},{x_2} = {140^0}$

Câu 11

Có bao nhiêu số tự nhiên có 3 chữ số đôi một khác nhau được lập từ các số 0,2,4,6,8:

A. 60

B. 40

C. 48

D. 10

Lời giải :

Một số gồm 3 chữ số phân biệt lập thành từ các chữ số A={0; 2; 4; 6; 8} có dạng:

$\overline {{a_1}{a_2}{a_3}}$ , với ${a_i} \in A,i = \overline {1,3} , {a_i} \ne {a_j},i \ne j.$

Do ${a_1} \ne 0$ - có $C_4^1 = 4$ cách chọn.

Khi đó 2 số ${a_{1,}}{a_2}$ được lấy từ 4 số còn lai sắp theo thứ tự nên có $A_4^2 = 12$ cách.

Số cách chọn là 4.12 = 48

Câu 12

Giá trị của $n \in \mathbb{N}$ thỏa mãn $C_{n + 8}^{n + 3} = 5A_{n + 6}^3$ là:

A. 6

B. 14

C. 15

D. 17

Lời giải :

Ta có

$\begin{array}{l}C_{n + 8}^{n + 3} = 5A_{n + 6}^3 \\\Leftrightarrow \dfrac{{\left( {n + 8} \right)!}}{{\left( {n + 3} \right)!.5!}} = 5.\dfrac{{\left( {n + 6} \right)!}}{{\left( {n + 3} \right)!}}\\ \Leftrightarrow \left( {n + 7} \right)\left( {n + 8} \right) = 5!.5\\ \Leftrightarrow {n^2} + 15n - 544 = 0 \\\Leftrightarrow n = 17(n > 0)\end{array}$

Câu 13

Gieo ngẫu nhiên một đồng tiền cân đối và đồng chất bốn lần. Xác suất để cả bốn lần gieo đều xuất hiện mặt sấp là:

A.

$\dfrac{4}{{16}}$

B.

$\dfrac{2}{{16}}$

C.

$\dfrac{1}{{16}}$

D.

$\dfrac{6}{{16}}$

Lời giải :

Số phần tử của không gian mẫu là: $\left| \Omega \right| = {2^4} = 16$

Gọi A là biến cố: “cả 4 lần đều xuất hiện mặt sấp”

Ta có: ${P_A} = \dfrac{1}{{16}}$

Câu 14

Xếp 6 người A, B, C, D, E, F vào một ghế dài . Hỏi có bao nhiêu cách sắp xếp sao cho A và F ngồi cạnh nhau:

A. 242

B. 240

C. 244

D. 248

Câu 15

Trong khai triển ${\left( {{a^2} + \dfrac{1}{b}} \right)^7}$ số hạng thứ 5 là:

A.

$35{a^6}.{b^{ - 4}}$

B.

$- 35{a^6}.{b^{ - 4}}$

C.

$35{a^4}.{b^{ - 5}}$

D.

$- 35{a^4}.{b^{}}$

Lời giải :

Số hạng thứ 5 $C_7^3{\left( {{a^2}} \right)^3}.{\left( {\dfrac{1}{b}} \right)^4} = 35{a^6}.{b^{ - 4}}$

Câu 16

Có tất cả 120 cách chọn 3 học sinh từ nhóm n (chưa biết) học sinh. Số n là nghiệm của phương trình nào sau đây:

A.

$n(n + 1)(n + 2) = 120$

B.

$n(n - 1)(n - 2) = 120$

C.

$n(n + 1)(n + 2) = 720$

D.

$n(n - 1)(n - 2) = 720$

Lời giải :

Số cách chọn 2 học sinh từ nhóm n học sinh là:

$C_n^1.C_n^2.C_n^3$ $= \dfrac{{n!}}{{\left( {n - 1} \right)!}}.\dfrac{{n!}}{{2!\left( {n - 2} \right)!}}.\dfrac{{n!}}{{3!\left( {n - 3} \right)!}}$ $= \dfrac{1}{6}n\left( {n - 1} \right)\left( {n - 2} \right)$

Theo bài ra ta có 120 cách lựa chọn nên:

$\dfrac{1}{6}n\left( {n - 1} \right)\left( {n - 2} \right) = 120$ $\Leftrightarrow n\left( {n - 1} \right)\left( {n - 2} \right) = 720$

Câu 17

Cho hai biến số A và B có $P(A) = \dfrac{1}{3}\,,P(B) = \dfrac{1}{4}\,,\,P(A \cup B) = \dfrac{1}{2}$ . Ta kết luận hai biến cố A và B là:

A. Độc lập

B. Không xung khắc

C. Xung khắc

D. Không rõ

Lời giải :

Ta có $P(A) + P(B) = \dfrac{1}{{12}}\, \ne P(A \cup B) = \dfrac{1}{2}$

Câu 18

Một bình đựng 4 quả cầu xanh và 6 quả cầu trắng. Chọn ngẫu nhiên 3 quả cầu. Xác suất để được 3 quả cầu toàn màu xanh là:

A.

$\dfrac{1}{{20}}$

B.

$\dfrac{1}{{30}}$

C.

$\dfrac{1}{{15}}$

D.

$\dfrac{3}{{10}}$

Lời giải :

Ta có $n\left( \Omega \right) = C_{10}^3 = 120$

Gọi A là: “3 quả cầu toàn màu xanh”. Khi đó $n\left( A \right) = C_4^3 = 4$

Suy ra $P\left( A \right) = \dfrac{4}{{120}} = \dfrac{1}{{30}}$

Câu 19

Một thầy giáo có 5 cuốn sách toán, 6 cuốn sách văn, 7 cuốn sách Anh văn và các cuốn sách đôi một khác nhau. Thầy giáo muốn tặng 6 cuốn sách cho 6 học sinh. Hỏi thầy giáo có bao nhiêu cách tặng nếu thầy giáo chỉ muốn tặng một hoặc hai thể loại:

A. 2233440

B. 2573422

C. 2536374

D. 2631570

Lời giải :

Có $C_{13}^6 = 1716$ cách chọn để không có cuốn sách toán nào.

Có $C_{12}^6 = 924$ cách chọn để không có cuốn sách văn nào.

Có $C_{11}^6 = 462$ cách chọn để không có cuốn sách anh nào.

Do 6 học sinh là khác nhau nên có 6! cách tặng.

Vậy có 6!.(1716 + 924 + 462) = 2233440.

Câu 20

Một nhóm có 5 nam và 3 nữ. Chọn ra 3 người sao cho trong đó có ít nhất 1 nữ. Hỏi có bao nhiêu cách:

A. 46

B. 69

C. 48

D. 40

Lời giải :

Ta có $n\left( \Omega \right) = C_8^3 = 56$

Gọi A là: “3 người được chọn có ít nhất 1 nữ”.

Gọi $\overline A$ là: “3 người được chọn không có nữ”. Khi đó $n\left( {\overline A } \right) = C_5^3 = 10$

Suy ra $n\left( A \right) = n\left( \Omega \right) - n\left( {\overline A } \right) = 56 - 10 = 46$

Câu 21

Từ tập $A = \left\{ {0,1,2,3,4,5,6} \right\}$ ta có thể lập được bao nhiêu số tự nhiên gồm 4 chữ số đôi một khác nhau:

A. 720

B. 261

C. 235

D. 679

Lời giải :

Một số gồm 4 chữ số phân biệt lập thành từ các chữ số A={0; 1; 2; 3; 4; 5; 6} có dạng:

$\overline {{a_1}{a_2}{a_3}{a_4}}$ , với ${a_i} \in A,i = \overline {1,4}$ và ${a_i} \ne {a_j},i \ne j.$

Do ${a_1} \ne 0$ - có $C_6^1 = 6$ cách chọn.

Khi đó 2 số ${a_2},{a_3},{a_4}$ được lấy từ 6 số còn lai sắp theo thứ tự nên có $A_6^3 = 120$ cách.

Số cách chọn là 6.120 = 720

Câu 22

Một lớp có 20 nam và 26 nữ. Giáo viên chủ nhiệm cần chọn một ban cán sự gồm 3 người. Hỏi có bao nhiêu cách chọn nếu trong ban cán sự có cả nam và nữ.

A. 11440

B. 11242

C. 24141

D. 53342

Lời giải :

TH1: có 1 nữ và 2 nam, số cách chọn là: $C_{26}^1.C_{20}^2 = 4940$

TH2: có 2 nữ và 1 nam, số cách chọn là: $C_{26}^2.C_{20}^1 = 6500$

Vậy có cách chọn thỏa mãn. 4940 + 6500 = 11440

Câu 23

Cho P, Q cố định và phép tịnh tiến T biến điểm M bất kỳ thành ${M_2}$ sao cho $\overrightarrow {M{M_2}} = 2\overrightarrow {PQ}$ . Chọn kết luận đúng

A. T là phép tịnh tiến theo vectơ

$\overrightarrow {PQ}$

B. T là phép tịnh tiến theo vectơ

$\overrightarrow {M{M_2}}$

C. T là phép tịnh tiến theo vectơ

$2\overrightarrow {PQ}$

D. T là phép tịnh tiến theo vectơ

${1 \over 2}\overrightarrow {PQ}$

Lời giải :

Gọi ${T_{\vec v}}\left( M \right) = {M_2} \Leftrightarrow \overrightarrow {M{M_2}} = \vec v$

Từ $\overrightarrow {M{M_2}} = 2\overrightarrow {PQ} \Rightarrow 2\overrightarrow {PQ} = \vec v$

Câu 24

Trong mặt phẳng Oxy, phép tịnh tiến theo vectơ $\vec v = (1;3)$ biến điểm A (1;2) thành điểm nào trong các điểm sau đây?

A. (2;5)

B. (1;3)

C. (3;4)

D. (- 3;4)

Lời giải :

${T_{\vec v}}\left( A \right) = B \Leftrightarrow \overrightarrow {AB} = \vec v$ $\Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{x_B} = 1 + 1 = 2}\\{{y_B} = 2 + 3 = 5}\end{array}} \right. \Rightarrow B\left( {2;5} \right)$

Câu 25

Giả sử rằng qua phép đối xứng trục ( a là trục đối xứng ), đường thẳng d biến thành đường thẳng $d'$ . Hãy chọn câu sai trong các câu sau?

A. Khi d song song với a thì d song song với d'.

B. d vuông góc với a thì d trùng với d'.

C. Khi d cắt a thì d cắt d'. Khi đó giao điểm của d và d' nằm trên a.

D. Khi d tạo với a một góc

${45^0}$ thì d vuông góc với d'.

Câu 26

Trong mặt phẳng Oxy, cho điểm M (1;5). Tìm ảnh của M qua phép đối xứng trục Ox.

A.

$M'( - 1;5)$

B.

$M'( - 1; - 5)$

C.

$M'(1; - 5)$

D.

$M'(0; - 5)$

Lời giải :

Gọi $M'(x';y')$ là ảnh của M qua Đ_Ox

Khi đó $\left\{ \begin{array}{l}x' = 1\\y' = - 5\end{array} \right. \Rightarrow M'\left( {1; - 5} \right)$

Câu 27

Trong các mệnh đề sau mệnh đề nào đúng?

A. Phép đối xứng tâm không có điểm nào biến thành chính nó.

B. Phép đối xứng tâm có đúng một điểm biến thành chính nó.

C. Có phép đối xứng tâm có hai điểm biến thành chính nó.

D. Có phép đối xứng tâm có vô số điểm biến thành chính nó.

Câu 28

Cho tam giác đều tâm O. Hỏi có bao nhiêu phép quay tâm O góc quay $\alpha ,0 < \alpha \le 2\pi$ biến tam giác trên thành chính nó?

A. Một

B. Hai

C. Ba

D. Bốn

Lời giải :

Có 3 phép quay tâm O góc $\alpha ,0 < \alpha \le 2\pi$ biến tam giác đều tâm O thành chính nó .

Đó là các phép quay với góc quay lần lượt bằng: $\dfrac{{2\pi }}{3},\dfrac{{4\pi }}{3},2\pi$

Câu 29

Cho đường thẳng d có phương trình x - y + 4 = 0. Hỏi trong các đường thẳng sau đường thẳng nào có thể biến thành d qua một phép đối xứng tâm?

A.

$2x + y - 4 = 0$

B.

$x + y - 1 = 0$

C.

$2x - 2y + 1 = 0$

D.

$2x + 2y - 3 = 0$

Câu 30

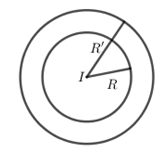
Cho hai đường tròn tâm \ $\left( {I;R} \right)$ và $\left( {I;R'} \right)\,\,\left( {R \ne R'} \right)$ . Có bao nhiêu phép vị tự biến đường tròn tâm $\left( {I;R} \right)$ thành đường tròn $\left( {I;R'} \right)?$

A. 0

B. 1

C. 2

D. Vô số

Lời giải :

Hai đường tròn đồng tâm I, có vô số phép vị tự tâm I tỉ số $k \ne \pm 1$ biến đường tròn này thành đường tròn kia.

Đề thi thử giữa học kỳ 1 môn Toán lớp 11 online - Mã đề 11

Trở thành Membership ngay

MEGA-AI phản hồi

Đăng nhập