Đề thi thử THPT QG năm 2022 môn Toán online - Đề thi của Trường THPT Phan Bội Châu
Vui lòng cài đặt đề thi trước khi làm bài
Cho cấp số cộng (un) biết u1=3,u2=−1. Tìm u3.
Đường cong trong hình vẽ bên là đồ thị hàm số nào dưới đây?
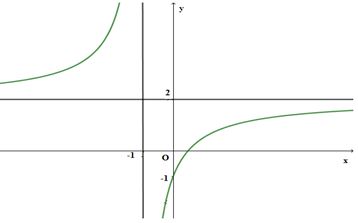
Tìm đường tiệm cận ngang của đồ thị hàm số y=2−2xx+1.
Cắt một khối trụ bởi một mặt phẳng qua trục của nó, ta được thiết diện là một hình vuông có cạnh bằng a. Tính diện tích xung quanh S của khối trụ đó.
Một mặt cầu có đường kính bằng a có diện tích S bằng bao nhiêu?
Tìm nghiệm của phương trình {\log _2}\left( {3x - 2} \right) = 3.
Cho biểu thức P = {2^x}{.2^y}\left( {x;y \in \mathbb{R}} \right). Khẳng định nào sau đây đúng?
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Tính thể tích V của khối chóp D'.ABCD.
Trong khai triển nhị thức {\left( {2x - 1} \right)^{10}}. Tìm hệ số của số hạng chứa {x^8}.
Cho hình chóp S.ABC có SA vuông góc với đáy ABC. Tam giác ABC vuông cân tại B và SA = a\sqrt 2 ,SB = a\sqrt 5 . Tính góc giữa SC và mặt phẳng \left( {ABC} \right).
Phương trình {\sin ^2}x + \sqrt 3 \sin x\cos x = 1có bao nhiêu nghiệm thuộc \left[ {0;2\pi } \right]?
Gọi M,m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = x + \sqrt {4 - {x^2}} . Tính M - m.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a\sqrt 2 . Biết SA vuông góc với đáy và SC = a\sqrt 5 . Tính thể tích V của khối chóp đã cho.
Cho hàm số y = f\left( x \right) có đồ thị như hình vẽ. Tìm khoảng đồng biến của hàm số.
Cho hai số thực a,b với a > 0,a \ne 1,b \ne 0. Khẳng định nào sau đây sai?
Cho hàm số f\left( x \right) có đạo hàm f'\left( x \right) = {x^2}{\left( {x + 1} \right)^3}\left( {x + 2} \right). Hàm số f\left( x \right) có mấy điểm cực trị?
Cho {\log _a}b = 2;{\log _a}c = 3. Tính giá trị của biểu thức P = {\log _a}\left( {a{b^3}{c^5}} \right)
Hàm số nào sau đây nghịch biến trên \mathbb{R}?
Gọi M,m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = x + \frac{1}{x} trên \left[ {\frac{1}{3};3} \right]. Tính 3M + 2m.
Gọi {x_1},{x_2} là nghiệm của phương trình {7^{{x^2} - 5x + 9}} = 343. Tính {x_1} + {x_2}.
Thiết diện qua trục của hình nón tròn xoay là một tam giác đều cạnh 2a. Tính thể tích V của khối nón đó.
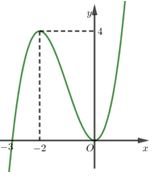
Cho hàm số y = a{x^4} + b{x^2} + c có đồ thị như hình vẽ. Mệnh đề nào sau đây đúng?
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng 2a. Tính bán kính R của mặt cầu ngoại tiếp hình chóp đã cho.
Cho lăng trụ tam giác đều, có độ dài tất cả các cạnh bằng 2. Tính thể tích V của khối lăng trụ đó.
Viết phương trình tiếp tuyến của đồ thị hàm số y = {x^3} - 3{x^2} + 1 biết nó song song với đường thẳng y = 9x + 6.
Cho lăng trụ ABC.A'B'C' có đáy là tam giác vuông tại A, AB = a,AC = a\sqrt 2 . Biết góc giữa mặt phẳng \left( {A'BC} \right) và mặt phẳng \left( {ABC} \right) bằng {60^0} và hình chiếu vuông góc của A' trên \left( {ABC} \right) là trung điểm H của AB. Tính thể tích V của khối lăng trụ đó.
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a,\widehat {ABC} = 60^\circ ,SA = SB = SC = a\sqrt 2 . Tính thể tích V của khối chóp đã cho.
Có bao nhiêu số nguyên dương m sao cho đường thẳng y = x + m cắt đồ thị hàm số y = \frac{{2x - 1}}{{x + 1}} tại hai điểm phân biệt A,B và AB \le 4?
Cho hình chóp S.ABC có đáy ABC là tam giác cân tại A, biết AB = a;SA = SB = a và mặt phẳng \left( {SBC} \right) vuông góc với mặt phẳng \left( {ABC} \right). Tính SC biết bán kính mặt cầu ngoại tiếp hình chóp S.ABC bằng a.
Cho hàm số f\left( x \right) = {x^3} - \left( {2m - 1} \right){x^2} + \left( {2 - m} \right)x + 2. Tìm tất cá các giá trị thực của tham số m để hàm số y = f\left( {\left| x \right|} \right) có 5 cực trị.
Cho hình trụ có bán kính đáy bằng a\sqrt 2 . Cắt hình trụ bởi một mặt phẳng, song song với trụ của hình trụ và cách trục của hình trụ một khoảng bằng \frac{a}{2} ta được thiết diện là một hình vuông. Tính thể tích V của khối trụ đã cho.
Cho tập hợp X gồm các số tự nhiên có 6 chữ số khác nhau có dạng \overline {abcdef} . Từ tập X lấy ngẫu nhiên một số. Tính xác suất để số lấy ra là số lẻ và thõa mãn a < b < c < d < e < f.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh a. SO vuông góc với mặt phẳng \left( {ABCD} \right) và SO = a\sqrt 2 . Tính khoảng cách d giữa SC và AB.
Tìm tất cả các giá trị khác nhau của tham số m để hàm số y = \frac{{{5^{ - x}} + 2}}{{{5^{ - x}} - m}} đồng biến trên \left( { - \infty ;0} \right).
Tìm tất cả các giá trị của tham số m để phương trình \left( {m + 3} \right){9^x} + \left( {2m - 1} \right){3^x} + m + 1 = 0 có hai nghiệm trái dấu.
Tìm tất cá các giá trị thực của tham số m để hàm số y = \frac{1}{3}{x^3} - 2m{x^2} + 4x - 5 đồng biến trên \mathbb{R}.
Tìm tất cả các giá trị của tham số m để phương trình {x^3} - 3{x^2} + 2 - m = 0 có ba nghiệm phân biệt.
Đặt a = {\log _7}11,b = {\log _2}7. Hãy biểu diễn {\log _{\sqrt[3]{7}}}\frac{{121}}{8} theo a và b.
Tìm tất cả các giá trị của tham số m để phương trình \log _2^2x + {\log _2}x - m = 0 có nghiệm x \in \left( {0;1} \right).
Cho hàm số y = f\left( x \right) có bảng xét dấu của đạo hàm như sau:
Hàm số y = 3f\left( {x + 3} \right) - {x^3} + 12x nghịch biến trên khoảng nào dưới đây?
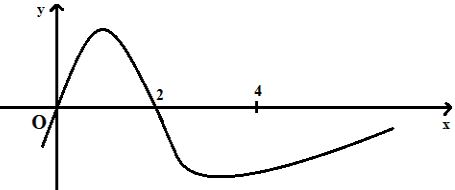
Giả sử hàm số y = f\left( x \right) có đạo hàm là hàm số y = f'\left( x \right) có đồ thị được cho như hình vẽ dưới đây và f\left( 0 \right) + f\left( 1 \right) - 2f\left( 2 \right) = f\left( 4 \right) - f\left( 3 \right). Tìm giá trị nhỏ nhất m của hàm số y = f\left( x \right) trên \left[ {0;4} \right].
Cho hai vị trí A, B cách nhau 615m , cùng nằm về một phía bờ song như hình vẽ. Khoảng cách từ A và từ B đến bờ song lần lượt là 118m và 487m. Một người đi từ A đến bờ song lấy nước mang về B. Tính đoạn đường ngắn nhất mà người ấy có thể đi.
Xét các số thực dương x,y thỏa mãn {\log _{\sqrt 3 }}\frac{{x + y}}{{{x^2} + {y^2} + xy + 2}} = x\left( {x - 3} \right) + y\left( {y - 3} \right) + xy. Tìm giá trị lớn nhất của biểu thức P = \frac{{3x + 2y + 1}}{{x + y + 6}} .
Cho lăng trụ ABC.A'B'C' có thể tích bằng 2. Gọi M,N lần lượt là hai điểm nằm trên cạnh AA',BB' sao cho M là trung điểm của AA' và BN = \frac{1}{2}NB'. Đường thẳng CM cắt đường thẳng C'A' tại P, đường thẳng CN cắt đường thẳng C'B' tại Q. Tính thể tích V của khối đa diện A'MPB'NQ.
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, SA vuông góc với mặt phẳng\left( {ABC} \right)và AB = 2,AC = 4,SA = \sqrt 5 . Mặt cầu đi qua các đỉnh của hình chóp S.ABC có bán kính là
Cho khối nón có bán kính đáy r = \sqrt 3 và chiều cao h = 4. Tính thể tích V của khối nón đã cho.
Tìm tập xác định D của hàm số y = {\left( {{x^2} - 3x - 4} \right)^{\sqrt {2 - \sqrt 3 } }}.
Cho a là số thực dương khác 5. Tính I = {\log _{\frac{a}{5}}}\left( {\dfrac{{{a^3}}}{{125}}} \right).
Cho a > 0, b > 0, giá trị của biểu thức T = 2{\left( {a + b} \right)^{ - 1}}.{\left( {ab} \right)^{\frac{1}{2}}}.{\left[ {1 + \dfrac{1}{4}{{\left( {\sqrt {\dfrac{a}{b}} - \sqrt {\dfrac{b}{a}} } \right)}^2}} \right]^{\frac{1}{2}}} bằng
Cho a, b, c dương và khác 1. Các hàm số y = {\log _a}x, y = {\log _b}x, y = {\log _c}x có đồ thị như hình vẽ

Khẳng định nào dưới đây đúng?


.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
