Thi thử trắc nghiệm online môn Toán - Đề thi thử THPT quốc gia 2020 Bộ Giáo dục và Đào tạo - Lần 2
Vui lòng cài đặt đề thi trước khi làm bài
. Có bao nhiêu cách chọn hai học sinh từ một nhóm gồm 10 học sinh ?
. Cho cấp số cộng $(u_{n})$ với $u_{1}=3$ và $u_{2}=9$ . Công sai của cấp số cộng đã cho bằng
. Nghiệm của phương trình $3 ^{x-1}=27$ là
. Thể tích của khối lập phương cạnh 2 bằng
. Tập xác định của hàm số $y=\log _{2} x$ là
. Hàm số $F(x)$ là một nguyên hàm của hàm số $f(x)$ trên khoảng K nếu
. Cho khối chóp có diện tích đáy B=3 và chiều cao h=4 . Thể tích của khối chóp đã cho bằng
. Cho khối nón có chiều cao $h=3$ và bán kính đáy $r=4$ . Thể tích của khối nón đã cho bằng
. Cho mặt cầu có bán kính $R=2$ . Diện tích của mặt cầu đã cho bằng
. Cho hàm số $f(x)$ có bảng biến thiên như sau. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
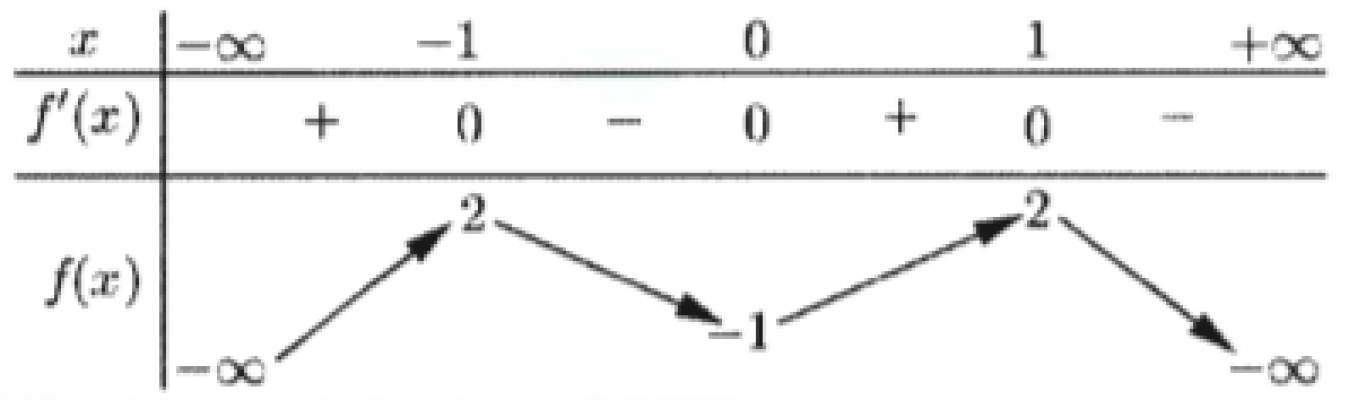
. Với a là số thực dương tùy ý, $\log _{2} ({a}^{3})$ bằng
. Diện tích xung quanh của hình trụ có độ dài đường sinh l và bán kính đáy r bằng
. Cho hàm số f(x) có bảng biến thiên như sau. Hàm số đã cho đạt cực đại tại
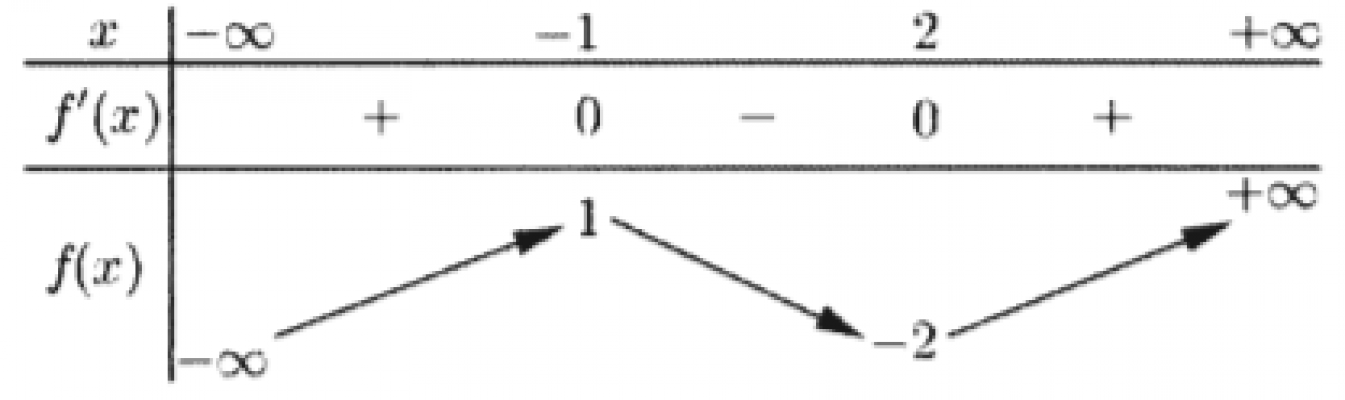
. Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên ?

. Tiệm cận ngang của đồ thị hàm số $y=\frac{x-2}{x+1}$ là
. Tập nghiệm của bất phương trình $\log {x} \geq 1$ là
. Cho hàm số bậc bốn y=f(x) có đồ thị trong hình bên. Số nghiệm của phương trình f(x) = -1 là
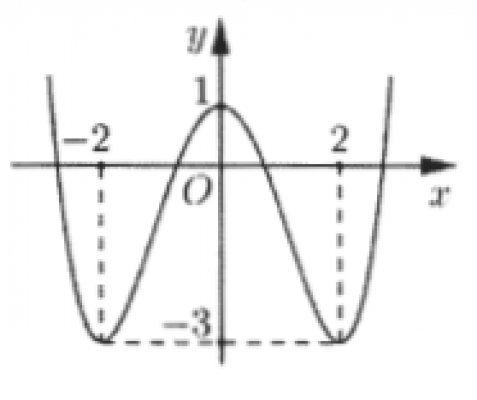
. Nếu $\int_{0}^{1} f(x) \mathrm{d} x=4$ thì $\int_{0}^{1} 2 f(x) \mathrm{d} x$ bằng
. Số phức liên hợp của số phức $z = 2 + i$ là
. Cho hai số phức $z_{1}=2+i$ và $z_{2}=1+3 i$. Phần thực của số phức $z_{1}+z_{2}$ bằng
. Trên mặt phẳng tọa độ, điểm biểu diễn số phức $z = -1 +2 i$ là điểm nào dưới đây ?
. Trong không gian Oxyz, hình chiếu vuông góc của điểm M(2 ; 1 ;-1) trên mặt phẳng (O z x) có tọa độ là
. Trong không gian Oxyz, cho mặt cầu $( S ): (x-2)^{2}+(y+4)^{2}+(z-1)^{2}=9$ . Tâm của $( S )$ có tọa độ là
. Trong không gian Oxyz, cho mặt phẳng $( P ) : 2 x+3 y+z+2=0$. Vectơ nào dưới đây là một vectơ pháp tuyến của $(P)$ ?
. Trong không gian Oxyz, cho đường thẳng $d: \frac{x-1}{2}=\frac{y-2}{3}=\frac{z+1}{-1}$. Điểm nào dưới đây thuộc d?
. Cho hình chóp $S.ABC$ có $SA$ vuông góc với mặt phẳng $(ABC), S A=a\sqrt{2} $, tam giác $A B C$ vuông cân tại $B$ và $A C=2 a$ (minh họa như hình bên). Góc giữa đường thẳng $S B$ và mặt phẳng $(A B C)$ bằng
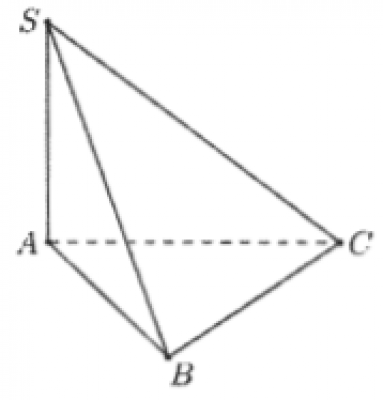
. Cho hàm số $f(x)$ có bảng xét dấu của $f^{\prime}(x)$ như sau. Điểm cực trị của hàm số đã cho là

. Giá trị nhỏ nhất của hàm số $f(x)=x^{4}-10 x^{2}+2$ trên đoạn $[-1 ; 2]$ bằng
. Xét các số thực a và b thỏa mãn $\log _{3}\left(3^{a} \cdot 9^{b}\right)=\log _{9} 3$ . Mệnh đề nào đưới đây đúng?
. Số giao điểm của đồ thị hàm số $y = x^{3}-3 x+1$ và trục hoành là
. Tập nghiệm của bất phương trình $9^{x}+2.3^{x}-3>0$ là
. Trong không gian, cho tam giác $ABC$ vuông tại $A, AB = a$ và $AC = 2a$. Khi quay tam giác $A B C$ xung quanh cạnh góc vuông $A B$ thì đường gấp khúc $A C B$ tạo thành một hình nón. Diện tich xung quanh của hình nón đó bằng
. Xét $\int_{0}^{2} x \mathrm{e}^{x^{2} } \mathrm{d} x$, nếu đặt $u=x^{2}$ thì $\int_{0}^{2} x \mathrm{e}^{x^{2} } \mathrm{d} x$ bằng
. Diện tích S của hình phẳng giới hạn bởi các đường $y=2 x^{2}, y=-1, x=0$ và $x=1$ được tính bởi công thức nào dưới đây ?
. Cho hai số phức $z_ {1}=3-i$ và $z_{2}=-1+i$ . Phần ảo của số phức $z_{1} z_{2}$ bằng
. Gọi z là nghiệm phức có phần ảo âm của phương trình $\bar{z}^{2}-2 \bar{z}+5=0$ . Môđun số phức $z_{0}+i$ bằng
. Trong không gian Oxyz, cho điểm $M(2 ; 1 ; 0)$ và đường thẳng $\Delta: \frac{x-3}{1}=\frac{y-1}{4}=\frac{z+1}{-2}$ phẳng đi qua $M$ và vuông góc với $\Delta$ có phương trình là
. Trong không gian $Oxyz$, cho hai điểm $M(1 ; 0 ; 1)$ và $N(3 ; 2 ;-1)$. Đường thẳng $M N$ có phương trình tham số là
. Có 6 chiếc ghế được kê thành một hàng ngang. Xếp ngẫu nhiên 6 học sinh, gồm 3 học sinh lớp A, 2 học sinh lớp B và 1 học sinh lớp C, ngồi vào hàng ghế đó, sao cho mỗi ghế có đúng một học sinh. Xác suất để học sinh lớp C chỉ ngồi cạnh học sinh lóp B bằng
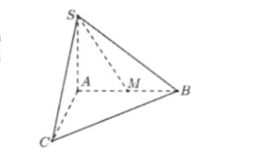
. Cho hình chóp $S . A B C$ có đáy là tam giác vuông tại $A A B=2 a, A C=4 a, S A$ vuông góc với mặt phẳng đáy và $S A=a$ như hình minh hoạ bên dưới. Gọi $M$ là trung điểm của $A B$. Khoảng cách giữa hai đường thẳng $S M$ và $B C$ bằng
. Có bao nhiêu giá trị nguyên của tham số m sao cho hàm số $f(x)=\frac{1}{3} x^{3}+m x^{2}+4 x+3$ đồng biến trên $\mathbb R$?
. Để quảng bá cho sản phẩm A, một công ty dự định tổ chức quảng cáo theo hình thức quảng cáo trên truyền hình. Nghiên cứu của công ty cho thấy: Nếu sau n lần quảng cáo được phát thì tỉ lệ người xem quảng cáo đó mua sản phẩm A tuân theo công thức $P(n)=\frac{1}{1+49 \mathrm{e}^{-0,015 n} }$ . Hỏi cần phát ít nhất bao nhiêu lần quảng cáo để tỉ lệ người xem mua sản phẩm đạt trên 30%?
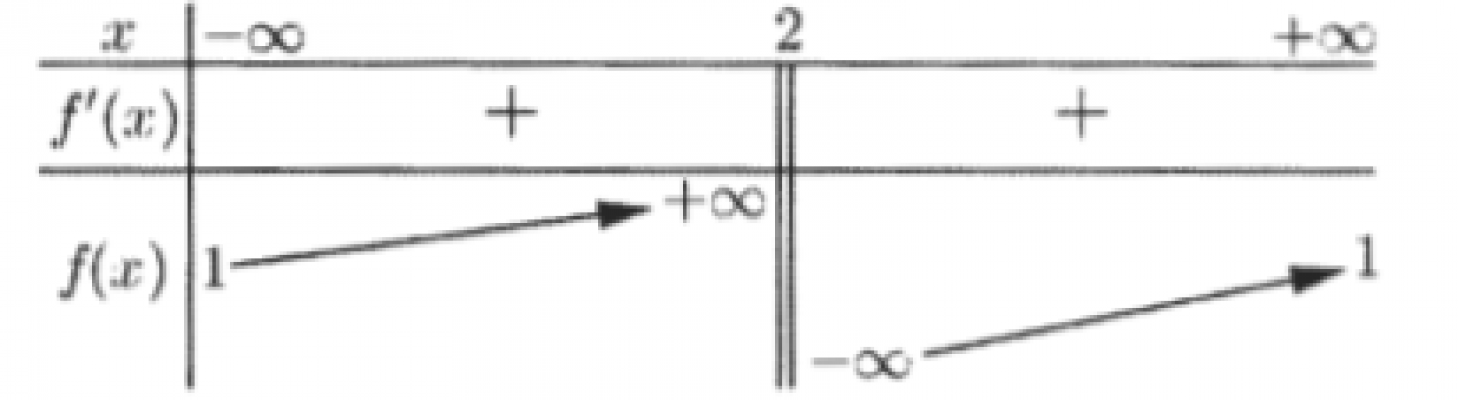
. Cho hàm số $f(x)=\frac{a x+1}{b x+c}(a, b, c \in \mathbb{R})$ có bảng biến thiên như sau. Trong các số $a, b$ và $c$ có bao nhiêu số dương?
. Cho hình trụ có chiều cao bằng 6a. Biết rằng khi cắt hình trụ đã cho bởi một mặt phẳng song song với trục và cách trục một khoảng bằng $3a$, thiết diện thu được là một hình vuông. Thể tích của khối trụ được giới hạn bởi hình trụ đã cho bằng
. Cho hàm số $f(x)$ có $f(0)=0$ và $f^{\prime}(x)=\cos x \cos ^{2} 2 x, \forall x \in \mathbb{R}$ . Khi đó $\int_{0}^{\pi} f(x) d x$ bằng
. Cho hàm số $f(x)$ có bảng biến thiên như sau. Số nghiệm thuộc đoạn $\left[0 ; \frac{5 \pi}{2}\right]$ của phương trình $f(\sin x)=1$ là

. Xét các số thực dương $a, b, x, y$ thỏa mãn $a>1, b>1$ và $a^{x}=b^{y}=\sqrt{a b}$ . Giá trị nhỏ nhất của biểu thức $P=x+2 y$ thuộc tập hợp nào dưới đây ?
. Cho hàm số $f(x)=\frac{x+m}{x+1}$ với m là tham số thực. Gọi $S$ là tập hợp tất cả các giá trị của m sao cho $\max _{[0,1]}|f(x)|+\min _{[0,1]}|f(x)|=2$ . Số phần tử của $S$ là
. Cho hình hộp $ABCD.A' B'C'D'$ có chiều cao bằng 8 và diện tích đáy bằng 9. Gọi $M, N, P$ và $Q$ lần lượt là tâm của các mặt bên $A B B^{\prime} A^{\prime}, B C C^{\prime} B^{\prime}, C D D^{\prime} C^{\prime}$ và $DAA^{\prime} D^{\prime}$. Thể tích của khối đa diện lồi có các đỉnh là các điểm $A, B, C, D, M, N, P$ và $Q$ bằng
. Có bao nhiêu số nguyên $x$ sao cho tồn tại số thực $y$ thỏa mãn $\log{3}(x+y)=\log {4}\left(x^{2}+y^{2}\right)$

