Thi thử trắc nghiệm online môn Toán - Đề thi chính thức THPT quốc gia 2019 - Mã đề 103
Vui lòng cài đặt đề thi trước khi làm bài
. Trong không gian Oxyz, cho mặt phẳng $(P): 2x-3y+z-2=0$. Vec tơ nào dưới đây là một vec tơ pháp tuyến của (P)?
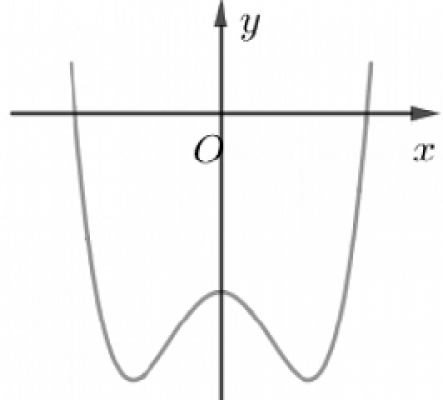
. Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên?
. Số cách chọn 2 học sinh từ 6 học sinh là
. Biết $\int_1^2 f(x)dx=2$ và $\int_1^2 g(x)dx=6$, khi đó $\int_1^2 [f(x)-g(x)]dx$ bằng
. Nghiệm của phương trình $2^{2x-1} = 8$ là
. Thể tích của khối nón có chiều cao h và bán kính đáy r là
. Số phức liên hợp của số phức $1-2i$ là
. Thể tích khối lăng trụ có diện tích đáy B và chiều cao h là
. Cho hàm số f(x) có bảng biến thiên như sau. Hàm số đã cho đạt cực đại tại
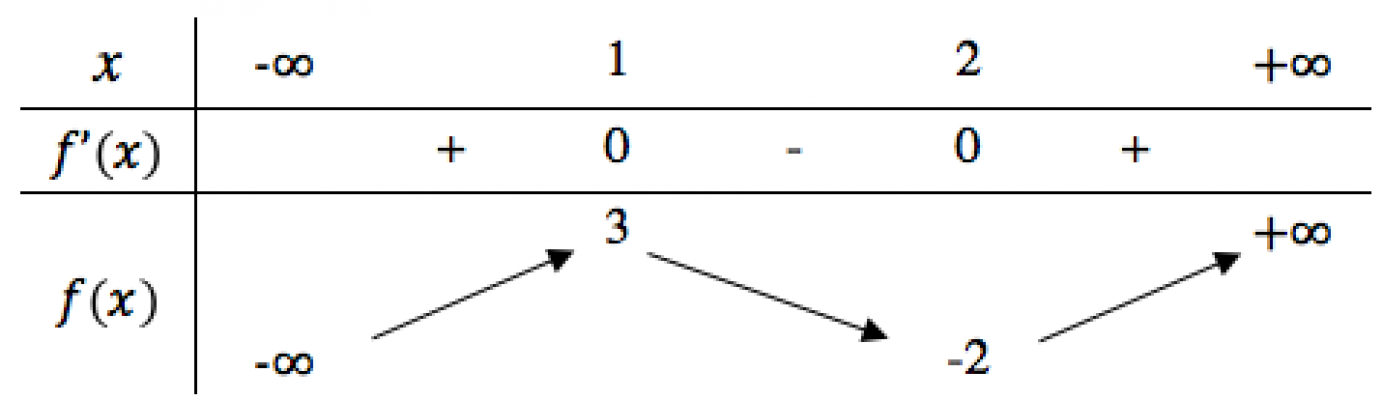
. Trong không gian Oxyz, hình chiếu vuông góc của điểm $M(2;1;-1)$ trên trục Oy có tọa độ là
. Cho cấp số cộng $(u_n)$ với $u_1=2$ và $u_2=6$. Công sai của cấp số cộng đã cho bằng
. Họ tất cả các nguyên hàm của hàm số $f(x)=2x+3$ là
. Trong không gian $Oxyz$, cho đường thẳng $d: {x+2\over1}={y-1\over-3}={z-3\over2}$. Vec tơ nào dưới đây là một vec tơ chỉ phương của $d$?
. Với a là số thực dương tùy ý, $\log_2a^3$ bằng
. Cho hàm số $f(x)$ có bảng biến thiên như sau. Hàm số đã cho đồng biến trên khoảng nào dưới đây?
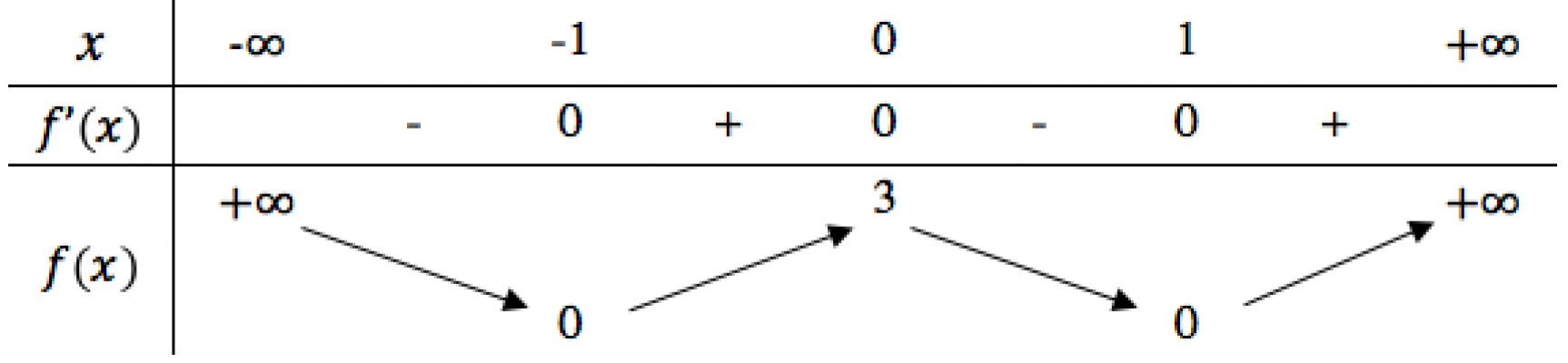
. Cho hàm số $f(x)$ có bảng biến thiên như sau. Số nghiệm thực của phương trình $2f(x)-3=0$ là?
. Cho hai số phức $z_1=1+i$ và $z_2=2+i$. Trên mặt phẳng tọa độ Oxy, điểm biểu diễn số phức $z_1+2z_2$ có tọa độ là
. Hàm số $y=2^{x^2-x}$ có đạo hàm là
. Giá trị lớn nhất của hàm số $f(x)=x^3-3x$ trên đoạn $[-3;3]$ bằng
. Cho hàm số $f(x)$ có đạo hàm $f'(x)=x(x-1)^2, \forall x \in \mathbb{R}$. Số điểm cực trị của hàm số đã cho là
. Cho hai số thực dương thỏa mãn $a^2b^3=16$. Giá trị của $2\log_2a+3\log_2b$ bằng
. Cho hình chóp $S.ABC$ có $SA$ vuông góc với mặt phẳng $(ABC), SA=\sqrt2a$, tam giác $ABC$ vuông cân tại $B$ và $AB=a$ minh họa như hình vẽ bên dưới. Góc giữa đường thẳng $SC$ và mặt phẳng $(ABC)$ bằng
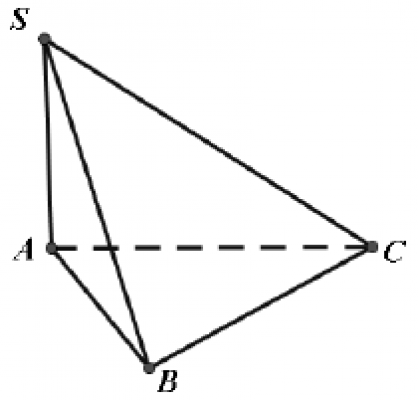
. Một cơ sở sản xuất có hai bể nước hình trụ có chiều cao bằng nhau, bán kính đáy lần lượt bằng 1m và 1,8m. Chủ cơ sỏ dự định làm một bể nước mới, hình trụ, có cùng chiều cao và có thể tích bằng tổng thể tích của hai bể nước trên. Bán kính đáy của bể nước dự định làm gần nhất với kết quả nào dưới đây?
. Nghiệm của phương trình $\log_2(x+1)+1 = \log_2(3x-1)$ là
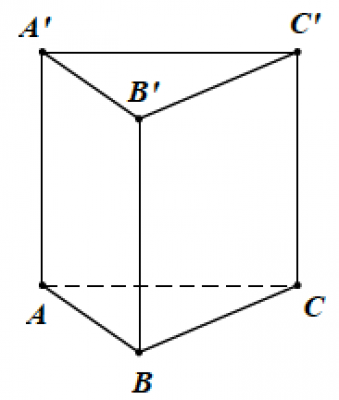
. Cho khối lăng trụ đứng $ABC.A'B'C'$ có đáy là tam giác đều cạnh $2a$ và $AA'=3a$ minh họa như hình vẽ bên dứoi. Thể tích của khối lăng trụ đã cho bằng
. Trong không gian Oxyz, cho mặt cầu $(S): x^2+y^2+z^2+2y-2z-7=0$. Bán kính của mặt cầu đã cho bằng
. Trong không gian $Oxyz$, cho hai điểm $A(2;1;2)$ và $B(6;5;-4)$. Mặt phẳng trung trực của đoạn thẳng AB có phương trình là
. Cho hàm số $y=f(x)$ có bảng biến thiên như sau. Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
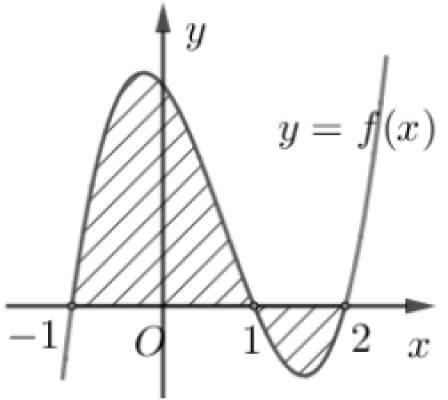
. Cho hàm số $f(x)$ liên tục trên $\mathbb{R}$. Gọi $S$ là diện tích hình phẳng giới hạn bởi các đường $y=f(x), y=0,x=-1$ và $x=2$ như hình vẽ bên dưới. Mệnh đề nào dưới đây là đúng?
. Gọi $z_1,z_2$ là hai nghiệm phức của phương trình $z^2-4z+5=0$. Giá trị của $z_1^2+z_2^2$ bằng
. Trong không gian Oxyz, cho các điểm $A(0;0;2), B(2;1;0), C(1;2;-1) và D(2;0;-2)$. Đường thẳng đi qua $A$ và vuông góc với mặt phẳng $(BCD)$ có phương trình là
. Cho số phức z thỏa mãn $(2+i)z - 4(\bar{z}-i) =. 8+19i$. Môđun của $z$ bằng
. Cho hàm số $f (x)$, bảng xét dấu của $f'(x)$ như sau. Hàm số $y=f(3-2x)$ đồng biến trên khoảng nào dưới đây?
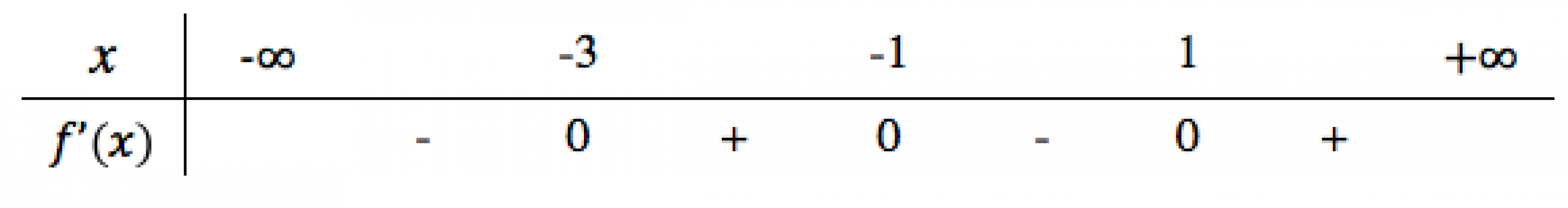
. Họ tất cả các nguyên hàm của hàm số $f(x)= {2x+1\over (x+2)^2}$ trên khoảng $(-2;+\infty)$ là
. Cho hàm số $f(x)$. Biết $f(0)=4$ và $f'(x)=2\sin^2x+1$, $\forall x \in\mathbb{R}$, khi đó $\int_0^{\pi\over4}f(x)dx$ bằng
. Cho phương trình $\log_9 x^2 - \log_3 (5x -1) = -\log_3 m$ với m là tham số thực. Có tất cả bao nhiêu giá trị nguyên của $m$ để phương trình đã cho có nghiệm?
. Cho hình trụ có chiều cao bằng $3\sqrt2$. Cắt hình trụ đã cho bởi mặt phẳng song song với trục và cách trục một khoảng bằng 1, thiết diện thu được có diện tích bằng $12 \sqrt2$. Diện tích xung quanh của hình trụ đã cho bằng
. Cho hàm số $y=f(x)$, hàm số $y=f'(x)$ liên tục trên và có đồ thị như hình vẽ bên. Bất phương trình $f(x)<2x+m$ với m là tham số thực, nghiệm đúng với mọi $x\in(0;2)$ khi và chỉ khi
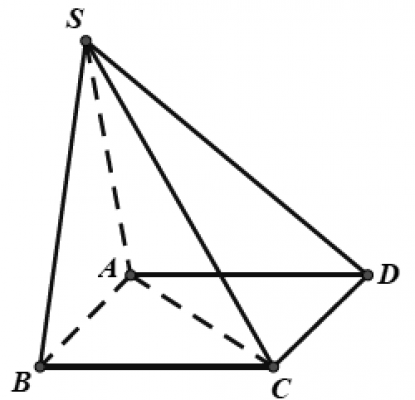
. Cho hình chóp $S.ABCD$ có đáy là hình vuông cạnh $a$, mặt bên $SAB$ là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy, minh họa như hình vẽ bên dưới. Khoảng cách từ $D$ đến mặt phẳng $(SAC)$ bằng
. Chọn ngẫu nhiên hai số khác nhau từ 21 số nguyên dương đầu tiên. Xác suất để chọn được hai số có tổng là một số chẵn bằng
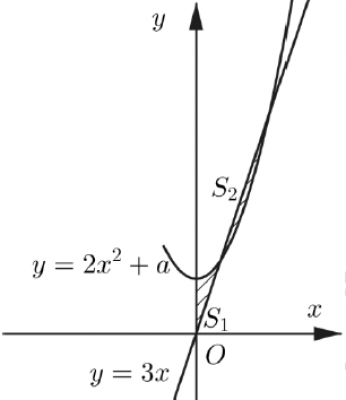
. Cho đường thẳng $y=3x$ và parabol $2x^2+a$ với a là tham số thực dương. Gọi $S_1$ và $S_2$ lần lượt là diện tích của hai hình phẳng được gạch chéo trong hình vẽ bên. Khi $S_1=S_2$ thì $a$ thuộc khoảng nào dưới đây?
. Trong không gian Oxyz, cho điểm $A(0;3; 2)$. Xét đường thẳng d thay đổi song song với $Oz$ và cách $Oz$ một khoảng bằng $2$. Khi khoảng cách từ $A$ đến $d$ nhỏ nhất. $d$ đi qua điểm nào dưới đây?
. Xét các số phức z thỏa mãn $|z|=\sqrt2$. Trên mặt phẳng tọa độ Oxy, tập hợp các điểm biểu diễn số phức $w={2+iz\over1+z}$ là một đường tròn có bán kính bằng
. Cho hàm số $f(x)$ có đạo hàm liên tục trên $\mathbb{R}$. Biết $f(6)=1$ và $\int_0^1xf(6x)dx=1$, khi đó $\int_0^6x^2f('(x)dx$ bằng
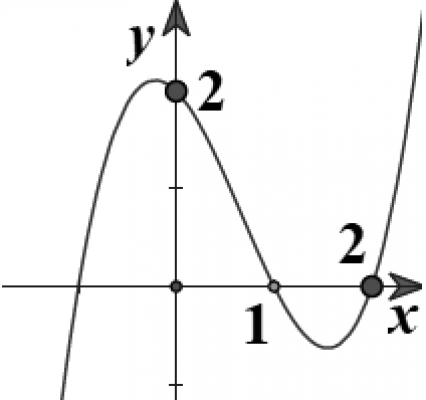
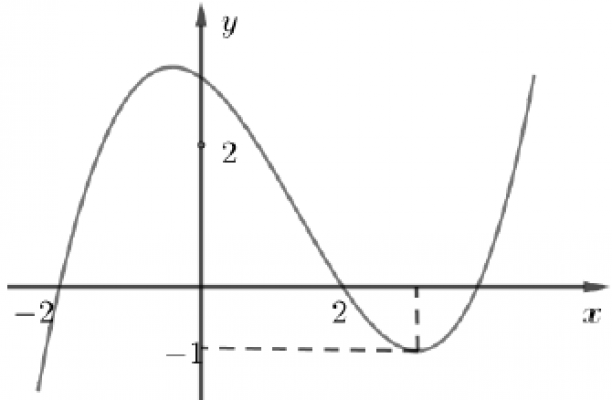
. Cho hàm số bậc ba $y=f(x)$ có đồ thị như hình vẽ dưới đây. Số nghiệm thực của phương trình $\left| f(x^3-3x) \right| = {3\over2}$ là
. Cho phương trình $(2\log_3^2 x -\log_3x-1)\sqrt{5^x-m} = 0$ với m là tham số thực. Có tất cả bao nhiêu giá trị nguyên dương của m để phương trình đã cho có đúng hai nghiệm phân biệt
. Trong không gian Oxyz, cho mặt cầu: $(S): x^2 + y^2 + (z+1)^2 = 5$. Có tất cả bao nhiêu điểm $A(a;b;c)$ trong đó a, b, c là các số nguyên, thuộc mặt phẳng Oxy sao cho có ít nhất hai tiếp tuyến của $(S)$ đi qua $A$ và hai tiếp tuyến đó vuông góc nhau?
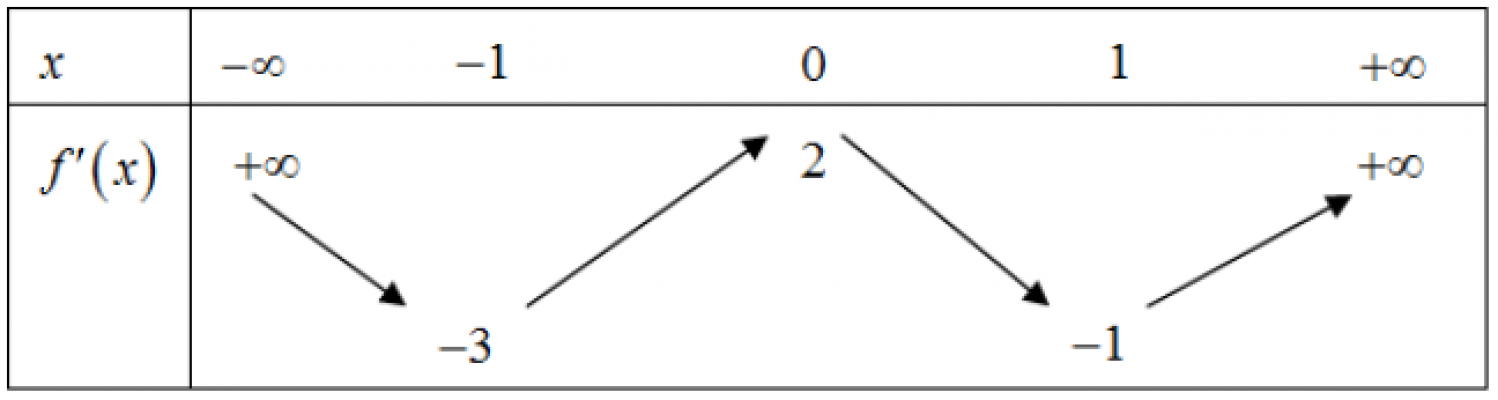
. Cho hàm số $f(x)$, bảng biến thiên của hàm số $f'(x)$ như sau. Số cực trị của hàm số $y=f(4x^2-4x)$ là
. Cho lăng trụ $ABC.A'B'C'$ có chiều cao bằng 6 và đáy là tam giác đều cạnh bằng 4. Gọi $M, N, P$ lần lượt là tâm các mặt bên $ABB'A', ACC'A', BCC'B'$. Thể tích khối đa diện lồi có các đỉnh là các điểm $A, B,C,M, N, P$ bằng
. Cho hai hàm số $y={x-1\over x} + {x\over x+1} + {x+1 \over x+2} + {x+2\over x+3} và y=|x+2|-x-m$ với m là tham số thực, có đồ thị lần lượt là $(C_1), (C_2)$. Tập hợp tất cả các giá trị của $m$ để $(C_1), (C_2) $cắt nhau tại đúng bốn điểm phân biệt là

