Đề thi thử tốt nghiệp THPT môn Toán năm 2023 online - Đề thi của Trường THPT Phú Lâm
Vui lòng cài đặt đề thi trước khi làm bài
Cho số phức $z=-1-2\sqrt{6}i$. Phần thực và phần ảo của số phức $\overline{z}$ là?
Đạo hàm của hàm số $y={{\log }_{2023}}\left( {{x}^{2}}+x \right)$ là
Đạo hàm của hàm số $y={{8}^{x}}$ là
Tìm tập nghiệm $S$ của bất phương trình ${{5}^{x+1}}-\frac{1}{5}>0$.
Tìm mệnh đề đúng trong các mệnh đề sau:
Cho tam giác $ABC$có trọng tâm $G$. Mệnh đề nào sau đây là mệnh đề SAI?
Số giao điểm của đồ thị $(C):y={{x}^{3}}-3{{x}^{2}}+2x+1$ và đường thẳng $y=1$ là
Cho hàm số $f\left( x \right)$ có đạo hàm trên đoạn $\text{ }\!\![\!\!\text{ }-1;\,2]$ và $f\left( -1 \right)=2023,\,f\left( 2 \right)=-1. $Tích phân $\int\limits_{-1}^{2}{{f}'\left( x \right)\text{d}x}$bằng:
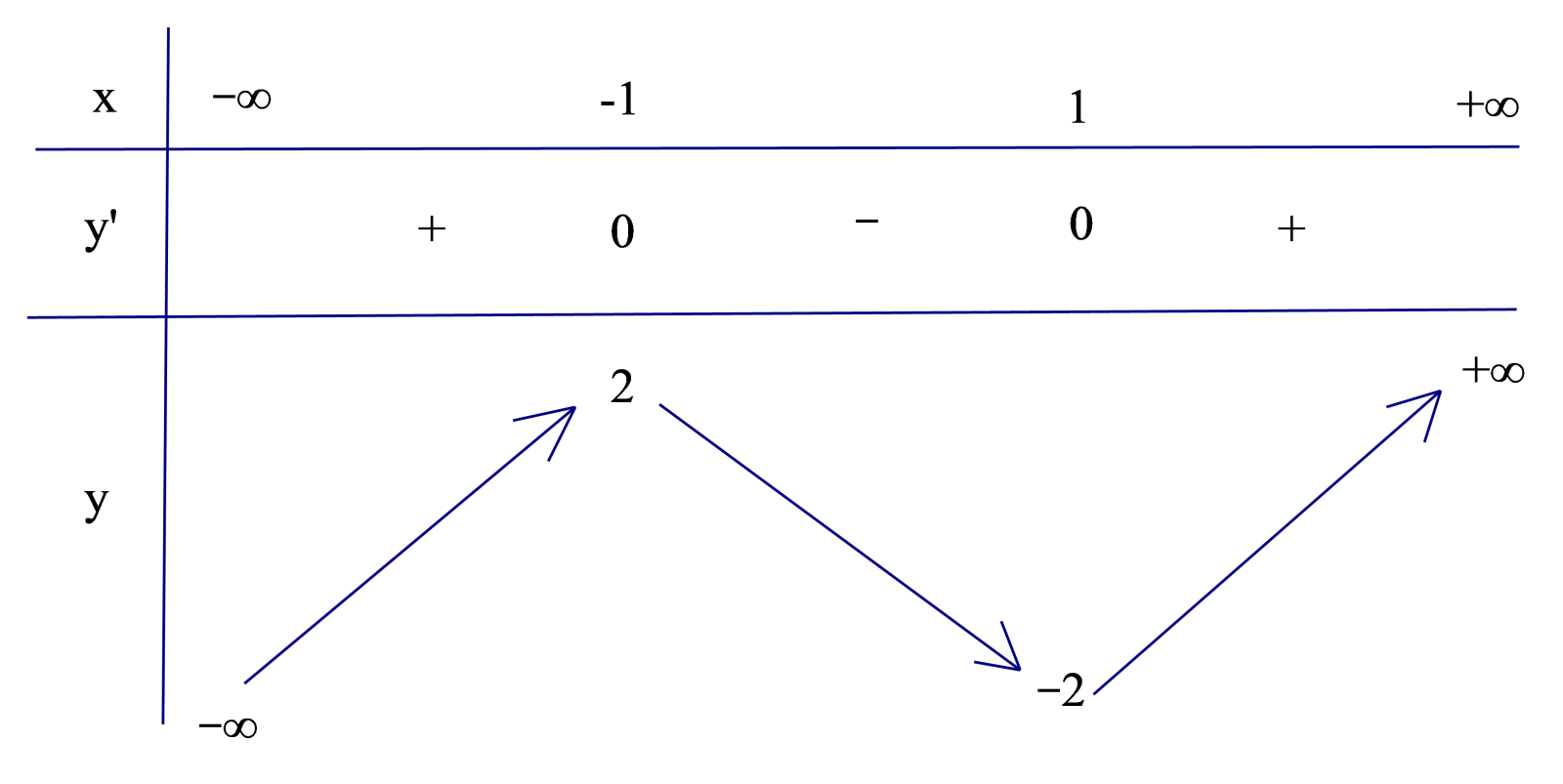
Hàm số nào dưới đây có bảng biến thiên như sau:
Trong không gian $Oxyz$, mặt cầu $\left( S \right):{{\left( x-1 \right)}^{2}}+{{\left( y-2 \right)}^{2}}+{{\left( z-3 \right)}^{2}}=25$ có tọa độ tâm $I$ và bán kính $R$ là
Cho điểm $M\left( 1,-4,-2 \right)$ và mặt phẳng $\left( P \right):x+y+5z-14=0$. Tính khoảng cách từ $M$ đến $(P)$.
Cho số phức $z$thỏa mãn $\left( 1+i \right)z=14-2i$. Tổng phần thực và phần ảo của $\overline{z}$ bằng
Thể tích của khối lăng trụ có diện tích đáy $S=2{{a}^{2}}$, chiều cao $h=6a$ là:
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$, $SA=a$ và $SA$ vuông góc với mặt phẳng đáy. Thể tích khối chóp $S.ABCD$ bằng
Phương trình tiếp tuyến của đường cong $y={{x}^{3}}+3{{x}^{2}}-2$ tại điểm có hoành độ ${{x}_{0}}=1$ là
Cho hai đường thẳng phân biệt $a$ và $b$ trong không gian. Có bao nhiêu vị trí tương đối giữa $a$ và $b$?
Cho hình trụ có bán kính đáy $r$ và độ dài đường sinh $l$. Diện tích xung quanh ${{S}_{xq}}$ của hình trụ đã cho được tính theo công thức nào dưới đây?
Trong không gian $\text{Ox}yz$, đường thẳng $d:\,\frac{x-1}{1}=\frac{y-3}{3}=\frac{z+4}{-2}$ đi qua điểm nào dưới đây?
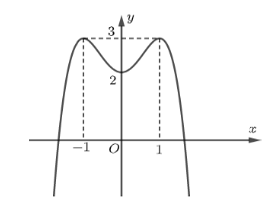
Cho hàm số $y=a{{x}^{4}}+b{{x}^{2}}+c$, $\left( a,b,c\in R \right)$ có đồ thị là đường cong như hình bên. Điểm cực tiểu của hàm số đã cho là:
Tiệm cận ngang của đồ thị hàm số $y=\frac{2x-1}{2x+4}$ là đường thẳng có phương trình:
Tập nghiệm của bất phương trình ${{3}^{{{x}^{2}}-13}}<27$ là
Có bao nhiêu số có năm chữ số khác nhau được tạo thành từ các chữ số 1,2,3,4,5,6?
Trong các mệnh đề sau, mệnh đề nào sai?
Cho hai tích phân $\int\limits_{-2}^{5}{f\left( x \right)\text{d}}x=8$ và $\int\limits_{5}^{-2}{g\left( x \right)\text{d}}x=3$. Tính $I=\int\limits_{-2}^{5}{\left[ f\left( x \right)-4g\left( x \right)-1 \right]\text{d}}x$
Cho $F(x)$ là một nguyên hàm của hàm số $f(x)$. Tìm $I=\int{\left[ 2f(x)+1 \right]}\text{d}x$.
:
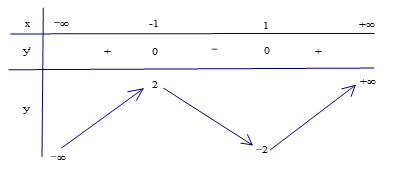
Hàm số nào dưới đây có bảng biến thiên như sau:
Cho hàm số $f\left( x \right)$ có đạo hàm$f'\left( x \right)=x\left( x-1 \right){{\left( x+4 \right)}^{2023}},\,\forall x\in \mathbb{R}$ . Số điểm cực trị của hàm số đã cho là
Đặt $a={{\log }_{2}}5,\,b={{\log }_{3}}5$. Hãy biểu diễn ${{\log }_{6}}5$theo $a$ và $b$.
Gọi S là diện tích hình phẳng giới hạn bởi các đồ thị hàm số: $y={{x}^{3}}-3x$, $y=x$. Tính S.=
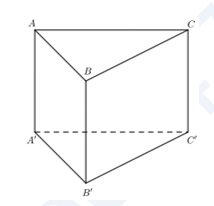
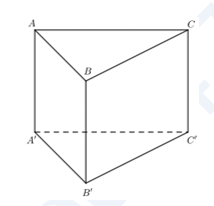
Cho hình lăng trụ đứng $ABC.{A}'{B}'{C}'$ có tất cả các cạnh bằng nhau. Góc giữa hai đường thẳng $A{B}'$ và $C{C}'$ bằng
Cho hàm số $f\left( x \right)=a{{x}^{4}}+b{{x}^{2}}+c$ có đồ thị là đường cong trong hình bên. Có bao nhiêu giá trị nguyên thuộc đoạn $\left[ -2;5 \right]$ của tham số $m$ để phương trình $f\left( x \right)=m$ có đúng hai nghiệm phân biệt?
Hàm số nào sau đây đồng biến trên $\mathbb{R}$?
Cho tứ diện $ABCD.$ Gọi $G$ là trọng tâm tam giác $BCD.$ Cặp đường thẳng nào sau đây cắt nhau?
Nghiệm của phương trình ${{\log }_{3}}\left( 2x+1 \right)=1+{{\log }_{3}}\left( x-1 \right)$ là
Gọi ${{z}_{1}}$ là nghiệm phức có phần ảo âm của phương trình ${{z}^{2}}-2z+5=0$. Tọa độ điểm biểu diễn số phức $\frac{7-4i}{{{z}_{1}}}$ trên mặt phẳng phức là
Trong không gian $Oxyz$, phương trình mặt phẳng $\left( P \right)$ song song và cách đều hai đường thẳng ${{d}_{1}}:\frac{x-2}{-1}=\frac{y}{1}=\frac{z}{1}$ và ${{d}_{2}}:\frac{x}{2}=\frac{y-1}{-1}=\frac{z-2}{-1}$ là
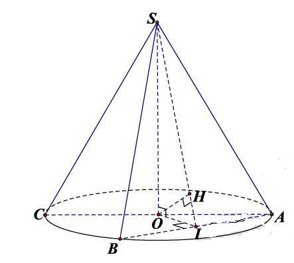
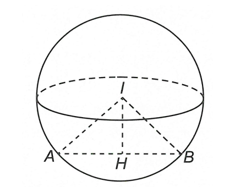
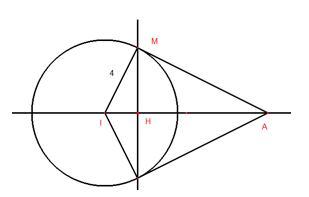
Cho hình nón đỉnh$S$, đáy là đường tròn $\left( O;\,5 \right)$.Một mặt phẳng đi qua đỉnh của hình nón cắt đường tròn đáy tại hai điểm $A$ và $B$ sao cho $SA=AB=8$. Tính khoảng cách từ $O$ đến $\left( SAB \right)$.
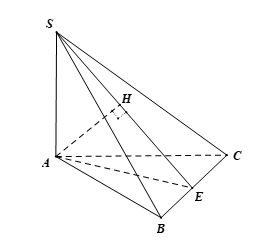
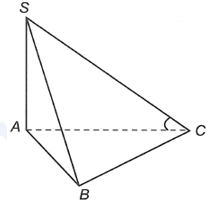
Cho hình chóp $S.ABC$có $SA=a$ và $SA$ vuông góc với đáy. Biết đáy là tam giác vuông cân tại $A$ và $BC=a\sqrt{2}$. Tính khoảng cách từ $A$ đến mặt phẳng $\left( SBC \right)$.
Khẳng định nào sau đây đúng?
Tập nghiệm của bất phương trình $({{3}^{2x}}-9)({{3}^{x}}-\frac{1}{27})\sqrt{{{3}^{x+1}}-1}\le 0$ chứa bao nhiêu số nguyên ?
Cho hàm số $f\left( x \right)$ xác định trên $\mathbb{R}\backslash \left\{ -1;1 \right\}$, thỏa mãn $f'\left( x \right)=\frac{2}{{{x}^{2}}-1};\ f\left( -3 \right)+f\left( 3 \right)=2\ln 2$ và $f\left( -\frac{1}{2} \right)+f\left( \frac{1}{2} \right)=0$. Giá trị của biểu thức $P=f\left( -2 \right)+f\left( 0 \right)+f\left( 4 \right)$ là:
Cho $I=\int\limits_{1}^{2}{\frac{{{x}^{2}}+{{\left( x+\ln x \right)}^{2}}+x}{{{x}^{2}}{{\left( x+\ln x \right)}^{2}}}\text{d}x}=\frac{a}{2}-\frac{1}{b+\ln c}$ với $a$, $b$, $c$ là các số nguyên dương. Khẳng định nào sau đây đúng ?
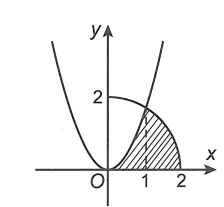
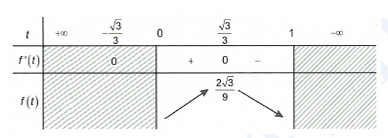
Cho $\left( H \right)$ là hình phẳng giới hạn bởi parabol $y=\sqrt{3}{{x}^{2}}$, cung tròn có phương trình $y=\sqrt{4-{{x}^{2}}}$ (với $0\le x\le 2$) và trục hoành (phần tô đậm trong hình vẽ). Diện tích của $\left( H \right)$ là
Cho hai số phức ${{z}_{1}}=2+i,{{z}_{2}}=1-2i.$ Môđun của số phức $w=\frac{z_{1}^{2022}}{z_{2}^{2023}}$ là
Cho hình trụ có thiết diện qua trục là một hình vuông. Thiết diện của hình trụ tạo bởi mặt phẳng song song và cách trục một khoảng bằng $a$ có diện tích bằng $8{{a}^{2}}\sqrt{3}$. Thể tích của khối trụ là
Trong không gian Oxyz, cho điểm $I\left( 1;-2;3 \right).$ Viết phương trình mặt cầu tâm I, cắt trục Ox tại hai điểm A và B sao cho $AB=2\sqrt{3}.$
Cho hai đường thẳng chéo nhau $a$ và $b$. Lấy hai điểm $A,B$ phân biệt thuộc $a$ và hai điểm $C,D$ phân biệt thuộc $b$. Khi đó hai đường thẳng $A\text{D}$ và $BC$ ở vị trí
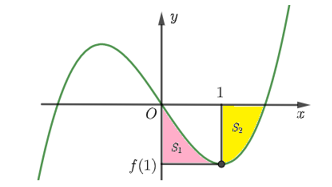
Cho hàm số bậc ba $y=f\left( x \right)$ có đồ thị như hình vẽ, biết $f\left( x \right)$ đạt cực tiểu tại điểm $x=1$ và thỏa mãn $\left[ f\left( x \right)+1 \right]$ và $\left[ f\left( x \right)-1 \right]$ lần lượt chia hết cho ${{\left( x-1 \right)}^{2}}$ và ${{\left( x+1 \right)}^{2}}$. Gọi ${{S}_{1}},{{S}_{2}}$ lần lượt là diện tích như trong hình bên. Tính $2{{S}_{2}}+8{{S}_{1}}$.
Cho hình chóp $S.ABC$ có đáy là tam giác $ABC$ vuông cân tại $C$ và $SA$ vuông góc với mặt phẳng đáy. Cho $SC=a$, mặt phẳng $\left( SBC \right)$ tạo với mặt đáy một góc $\alpha $. Thể tích khối chóp $S.ABC$ đạt giá trị lớn nhất là
Trong không gian Oxyz, cho mặt cầu $\left( S \right):\,{{\left( x-2 \right)}^{2}}+{{\left( y-3 \right)}^{2}}+{{\left( z+1 \right)}^{2}}=16$ và điểm $A\left( -1;-1;-1 \right).$ Xét các điểm M thuộc $\left( S \right)$sao cho đường thẳng AM tiếp xúc với $\left( S \right).$ M luôn thuộc một mặt phẳng cố định có phương trình là