Thi thử trắc nghiệm môn Lý thuyết điều khiển tự động online - Đề #1
Vui lòng cài đặt đề thi trước khi làm bài
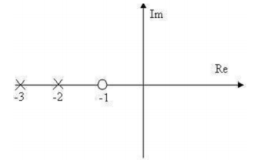
Hệ thống có các cực và zero như trên hình vẽ thì:
Hệ thống có hàm truyền: $G(s) = \frac{{3(s + 4)}}{{{s^2} + 2s + 1}}$
Hệ thống có hàm truyền hở thì hệ thống kính: $G(s) = \frac{{3(s + 4)}}{{{s^2} + 2s + 1}}$
Khâu hiệu chỉnh PID liên tục có dạng:
Hệ thống tuyến tính là hệ thống:
Yêu cầu đầu tiên đối với một hệ thống điều khiển tự động là:
Tìm nghiệm của hệ thống có phương trình đặc tính sau: ${s^2} + 6s + 5 = 0$
Cho hàm truyền hãy lập phương trình trạng thái.$G(s) = \frac{{20}}{{{s^2} + 2s + 8}}$
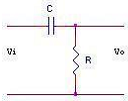
Hàm truyền đạt $G(s) = \frac{{{V_o}(s)}}{{{V_i}(s)}}$ của mạch điện ở hình sau là:
Hệ thống phi tuyến là hệ thống:
Biểu đồ Nyquist (đường cong Nyquist) là:
Khi thêm một cực có phần thực âm vào hàm truyền hệ hở thì:
Tìm số nhánh của qũi đạo nghiệm số của hệ thống hồi tiếp âm đơn vị có hàm truyền hệ hở là: $G(s) = \frac{{K(1 + 0.1s)}}{{{{(1 + 0.01s)}^2}}}$
ADC là:
ADC là:
Hàm truyền đạt $G(s) = \frac{{C(s)}}{{R(s)}}$ của hệ thống ở hình sau là:
Cho phương trình đặc trưng ${s^4} + 12,5{s^3} + {s^2} + 5s + K = 0$ . Hãy xác định K để hệ thống ổn định
Các cách đánh giá thường được dùng đề xét ổn định cho hệ liên tục là:
Cho hệ có phương trình đặc trưng ${s^4} + 2{s^3} + 3{s^2} + 4s + 5 = 0$ . Xét tính ổn định của hệ thống, và cho biết có bao nhiêu nghiệm bên trái, bao nhiêu nghiệm bên phải mặt phẳng phức:
Xét tính ổn định của hệ thống có phương trình đặc trưng: ${s^4} + 2{s^3} + 4{s^2} + 8s + 3 = 0$
Khâu hiệu chỉnh sớm trễ pha gồm:
Bản chất của biến đổi Z là:
Độ dự trữ pha:
Tín hiệu ra của bộ chuyển đổi A/D:
Tần số lấy mẫu: