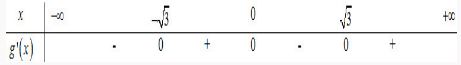Thi thử THPT quốc gia môn Toán online - Đề thi của Trường THPT Thanh Xuân năm 2022
Vui lòng cài đặt đề thi trước khi làm bài
Hàm số liên tục trên R và có bảng biến thiên như hình vẽ. Mệnh đề nào sau đây là đúng?
Cho hàm số $y = \dfrac{{2x}}{{x + 2}}$ có đồ thị $(C)$. Viết phương trình tiếp tuyến của $(C)$, biết tiếp tuyến tạo với hai trục tọa độ một tam giác có diện tích bằng $\dfrac{1}{{18}}$.
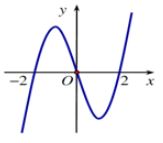
Cho hàm số$y = (x - 2)({x^2} - 5x + 6)$ có đồ thị $\left( C \right)$. Mệnh đề nào dưới đây đúng.
Hàm số $y = {x^4} - 8{x^2} - 4$ nghịch biến trên các khoảng.
Cho khai triển ${\left( {1 - 2x} \right)^n} = {a_0} + {a_1}x + {a_2}{x^2} + ... + {a_n}{x^n}$ biết $S = \left| {{a_1}} \right| + 2\left| {{a_2}} \right| + ... + n\left| {{a_n}} \right| = 34992$. Tính giá trị của biểu thức $P = {a_0} + 3{a_1} + 9{a_2} + ... + {3^n}{a_n}$
Số đường tiệm cận của đồ thị hàm số$y = \dfrac{{{x^2} - 3x + 2}}{{{x^2} - 4}}$ là.
Cho đồ thị của hàm số $y = {x^3} - 6{x^2} + 9x - 2$ như hình vẽ. Khi đó phương trình $\left| {{x^3} - 6{x^2} + 9x - 2} \right| = m$ (m là tham số) có 6 nghiệm phân biệt khi và chỉ khi.
Cho khối lập phương $ABCD.A'B'C'D'$ cạnh $a$. Các điểm E và $F$ lần lượt là trung điểm của C’B’ và C’D’. Mặt phẳng (AEF) cắt khối lập phương đã cho thành hai phần, gọi ${V_1}$ là thể tích khối chứa điểm A’ và ${V_2}$ là thể tích khối chứa điểm C’. Khi đó $\dfrac{{{V_1}}}{{{V_2}}}$ là.
Gọi $\left( {x;y} \right)$ là nghiệm dương của hệ phương trình $\left\{ \begin{array}{l}\sqrt {x + y} + \sqrt {x - y} = 4\\{x^2} + {y^2} = 128\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\end{array} \right.$. Tổng $x + y$ bằng:
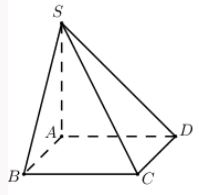
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật, $AB = a$. Cạnh bên $SA$ vuông góc với mặt phẳng $(ABCD)$ và $SA = a$. Góc giữa đường thẳng $SB$ và $CD$ là:
Gieo một con súc sắc cân đối, đồng chất một lần. Xác suất để xuất hiện mặt chẵn?
Số nghiệm nguyên của bất phương trình$\sqrt {2\left( {{x^2} - 1} \right)} \le x + 1$ là.
Phương trình tiếp tuyến với đồ thị hàm số $y = \dfrac{{x + 1}}{{x - 1}}$ song song với đường thẳng $\left( \Delta \right):\,\,2x + y + 1 = 0$ là.
:
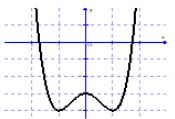
Đường cong trong hình vẽ bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi đó là hàm số nào?
:
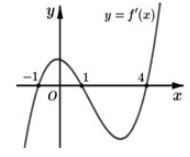
Cho hàm số $f\left( x \right)$ xác định trên R và có đồ thị hàm số $y = f'\left( x \right)$ là đường cong trong hình bên. Mệnh đề nào dưới đây đúng?
Một hộp đựng 11 tấm thẻ được đánh số từ 1 đến 11. Chọn ngẫu nhiên 6 tấm thẻ. Gọi $P$ là xác suất để tổng số ghi trên 6 tấm thẻ ấy là một số lẻ. Khi đó $P$ bằng.
Điểm cực tiểu của hàm số $y = {x^3} - 3{x^2} - 9x + 2$.
:
Cho hàm số $y = f(x)$ có bảng biến thiên như bên.
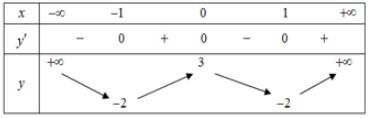
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. SA$ \bot $(ABCD) và $SB = \sqrt 3 $. Thể tích khối chóp S.ABCD là.
Phương trình tiếp tuyến của đồ thị hàm số $y = {x^3} - 3{x^2} - x + 3$ tại điểm $M\left( {1;0} \right)$ là.
Giá trị lớn nhất của hàm số $y = \dfrac{{{x^2} - 3x}}{{x + 1}}$ trên đoạn $\left[ {0;3} \right]$ bằng.
Cho hàm số $y = f\left( x \right) = \dfrac{1}{3}{x^3} - \left( {m + 1} \right){x^2} + \left( {m + 3} \right)x + m - 4$. Tìm để hàm số $y = f\left( {\left| x \right|} \right)$ có 5 điểm cực trị?
Đồ thị hàm số $y = \dfrac{{2x + 1}}{{x - 1}}$ có tiệm cận ngang là.
Số cách xếp 5 người vào 5 vị trí ngồi thành hàng ngang là.
Biết ${m_0}$ là giá trị của tham số m để hàm số $y = {x^3} - 3{x^2} + mx - 1$ có hai điểm cực trị ${x_1},\,\,{x_2}$ sao cho $x_1^2 + x_2^2 - {x_1}{x_2} = 13$. Mệnh đề nào dưới đây đúng?
Đồ thị sau đây là của hàm số nào?
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật, $AB = a,{\rm{ }}AD = 2a$, $SA$ vuông góc với mặt phẳng$\left( {ABCD} \right)$, $SA = a\sqrt 3 $. Thể tích của khối chóp $S.ABCD$ là.
Cho $\sin \alpha = \dfrac{1}{3}$và $\dfrac{\pi }{2} < \alpha < \pi $. Khi đó $\cos \alpha $ có giá trị là.
$\mathop {\lim }\limits_{x \to {1^ + }} \dfrac{{ - 2x + 1}}{{x - 1}}$ bằng.
Người ta muốn xây một bể chứa nước dạng hình hộp chữ nhật không nắp có thể tích bằng $200{m^3}$ đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng. Giá thuê nhân công xây bể là 300.000 đồng/m2. Chi phí thuê nhân công thấp nhất là.
Có bao nhiêu giá trị nguyên m để đường thẳng $\left( d \right):\,\,y = x - m$ cắt đồ thị hàm số $y = \dfrac{{x + 1}}{{x - 1}}$ tại hai điểm phân biệt A, B sao cho $AB = 3\sqrt 2 $.
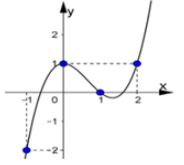
Cho hàm số $y = f\left( x \right)$có đồ thị như hình bên.
Tìm tất cả các giá trị thực của tham số $m$ để phương trình $f\left( x \right) = m + 2$ có bốn nghiệm phân biệt.
Gọi $S$là diện tích đáy, $h$là chiều cao. Thể tích khối lăng trụ là.
:
Cho hàm số $f(x)$ có đạo hàm $f'(x)$ có đồ thị như hình vẽ. Hàm số $g(x) = f(x) - \dfrac{{{x^3}}}{3} + {x^2} - x + 2$ đạt cực đại tại điểm nào?
Trong mặt phẳng với hệ toạ độ Oxy, cho tam giác ABC có đỉnh $B( - 12;1)$, đường phân giác trong góc A có phương trình $d:x + 2y - 5 = 0$. $G\left( {\dfrac{1}{3};\dfrac{2}{3}} \right)$ là trọng tâm tam giác ABC. Đường thẳng BC qua điểm nào sau đây.
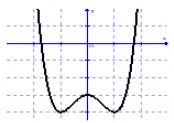
Đồ thị sau đây là của hàm số nào ?
Cho hình chóp tam giác $S.ABC$với $ABC$là tam giác đều cạnh $a$. $SA \bot (ABC)$ và $SA = a\sqrt 3 .$ Tính thể tích của khối chóp $S.ABC$.
Hỏi có tất cả bao nhiêu giá trị nguyên của m để đồ thị hàm số $y = 2{x^3} - 3\left( {m + 3} \right){x^2} + 18mx - 8$ tiếp xúc với trục hoành?
Gọi$S$ là tập hợp các số nguyên $m$ để hàm số $y = f(x) = \dfrac{{x + 2m - 3}}{{x - 3m + 2}}$ đồng biến trên khoảng $\left( { - \infty ; - 14} \right)$. Tính tổng $T$ của các phần tử trong $S$?
Cho khối chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $2a$. Hình chiếu vuông góc của $S$ trên mặt phẳng$\left( {ABCD} \right)$ là điểm $H$ thuộc đoạn $BD$ sao cho$HD = 3HB$. Biết góc giữa mặt phẳng $\left( {SCD} \right)$ và mặt phẳng đáy bằng${45^0}$. Khoảng cách giữa hai đường thẳng $SA$ và $BD$ là.
Hàm số $y = \dfrac{{2x - 1}}{{x + 1}}$. Khẳng định nào sau đây đúng.
Thể tích khối lăng trụ tam giác đều có tất cả các cạnh bằng a là.
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$, cạnh bên $SA$ vuông góc với đáy $\left( {ABCD} \right)$. Biết góc tạo bởi hai mặt phẳng $\left( {SBC} \right)$ và $\left( {ABCD} \right)$ bằng $60^\circ $. Tính thể tích $V$ của khối chóp $S.ABCD$.
Giá trị cực tiểu của hàm số $y = {x^4} - 2{x^2} - 3$là.
Phương trình $\cos x = \cos \dfrac{\pi }{3}$ có nghiệm là:
Hàm số $y = - {x^3} - 3{x^2} + 9x + 20$ đồng biến trên các khoảng.
Khoảng cách từ $I(1; - 2)$ đến đường thẳng $\Delta :3x - 4y - 26 = 0$ bằng.
Để giá trị lớn nhất của hàm số $y = \left| {\sqrt {2x - {x^2}} - 3m + 4} \right|$ đạt giá trị nhỏ nhất thì m thỏa.
Cho hàm số $y = f\left( x \right)$liên tục trên đoạn $\left[ { - 1;4} \right]$ và có đồ thị hàm số $y = f'\left( x \right)$ như hình bên. Hỏi hàm số $g\left( x \right) = f\left( {{x^2} + 1} \right)$ nghịch biến trên khoảng nào trong các khoảng sau?
Tính thể tích $V\;$của khối chóp có đáy là hình vuông cạnh $2a$ và chiều cao là $3a$

.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)

.JPG)
.JPG)
.JPG)