Đề thi thử tốt nghiệp THPT môn Toán năm 2023 online - Đề thi của Trường THPT Nguyễn Đình Chiểu
Vui lòng cài đặt đề thi trước khi làm bài
Cho mặt cầu $\left( S \right)$ có diện tích bằng $4\pi $. Thể tích khối cầu $\left( S \right)$ bằng:
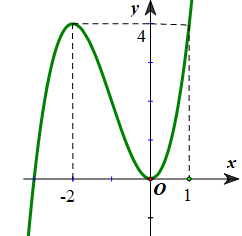
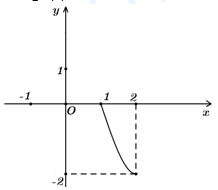
Cho hàm số $f\left( x \right)$ có đồ thị như hình vẽ bên dưới. Giá trị cực tiểu của hàm số bằng:
Trong không gian $Oxyz$, cho hai điểm $A\left( -2\,;-1\,;\,3 \right)$ và $B\left( 0\,;\,3\,;\,1 \right)$. Gọi $\left( \alpha \right)$ là mặt phẳng trung trực của đoạn $AB$. Một vec tơ pháp tuyến của $\left( \alpha \right)$ có tọa độ là:
:
Cho hàm số $y=f\left( x \right)$ có đồ thị như hình vẽ dưới đây.
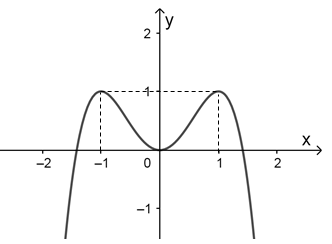
Mệnh đề nào sau đây đúng về hàm số đó?
Tập nghiệm của phương trình ${{\log }_{2}}x+{{\log }_{4}}x+{{\log }_{16}}x=7$ là
Họ nguyên hàm của hàm số $f\left( x \right)=\frac{1}{x}$ là
Cho khối lập phương có độ dài đường chéo bằng $\sqrt{3}$. Thể tích khối lập phương đó bằng:
Trong không gian $Oxyz,$ cho đường thẳng $d:\frac{x}{2}=\frac{y}{1}=\frac{z-1}{2}$. Một vectơ chỉ phương của $d$ là:
Môđun của số phức $z=(-4+3i).i$ bằng:
Cho cấp số nhân $\left( {{u}_{n}} \right)$có ${{u}_{1}}=1,\,\,{{u}_{2}}=-2$. Giá trị của ${{u}_{2019}}$ bằng
Cho $\int\limits_{0}^{1}{f(x)\text{d}x}=-3$ và $\int\limits_{0}^{1}{g(x)\text{d}x}=2$, khi đó $\int\limits_{0}^{1}{\left[ f\left( x \right)+2g\left( x \right) \right]\text{d}x}$ bằng
Đường cong trong hình bên là đồ thị của hàm số nào dưới đây?
Tập nghiệm của bất phương trình ${{\log }_{2}}\left( 4x+8 \right)-{{\log }_{2}}x\le 3$ là
Hàm số $y=f\left( x \right)$ có đạo hàm $f'\left( x \right)=\left( {{x}^{4}}-{{x}^{2}} \right){{\left( x+2 \right)}^{3}},\forall x\in \mathbb{R}$. Số điểm cực trị của hàm số là
Cho số phức $z$ thỏa mãn $z+2i.\overline{z}=1+17i$. Khi đó $\left| z \right|$ bằng
Trong không gian $Oxyz$, khoảng cách giữa: $\left( P \right):x+2y+2z=0$ và $\left( Q \right):x+2y+2z-12=0$ bằng
Ký hiệu ${{z}_{1}},\text{ }{{z}_{2}}$ là hai nghiệm phức của phương trình ${{z}^{2}}+2z+11=0$. Khi đó giá trị biểu thức $A={{\left| {{z}_{1}} \right|}^{2}}+{{\left| {{z}_{2}} \right|}^{2}}$ bằng:
Trong không gian $Oxyz$, mặt cầu tâm $I\left( -1;2;-3 \right)$ và đi qua điểm $A\left( 2;0;0 \right)$ có phương trình là:
Diện tích hình phẳng giới hạn bởi đồ thị của các hàm số $y=2{{x}^{2}}+x+1$ và $y={{x}^{2}}+3$ bằng:
Tìm tham số $m$ để đồ thị hàm số $y=\frac{\left( m+1 \right)x-5m}{2x-m}$ có tiệm cận ngang là đường thẳng $y=1$
Cho hình chóp tứ giác $S.ABCD$ có $SA=SB=SC=SD=4\sqrt{11}$. Đáy $ABCD$ là hình vuông cạnh $8$. Thể tích của khối chóp $S.ABC$ bằng
Tỉ số thể tích giữa khối lập phương và khối cầu ngoại tiếp khối lập phương đó bằng
Cho hai số thực $a$,$b$ thoả mãn $2{{\log }_{3}}\left( a-2b \right)={{\log }_{3}}a+{{\log }_{3}}b$ và $a>2b>0$. Khi đó $\frac{a}{b}$ bằng
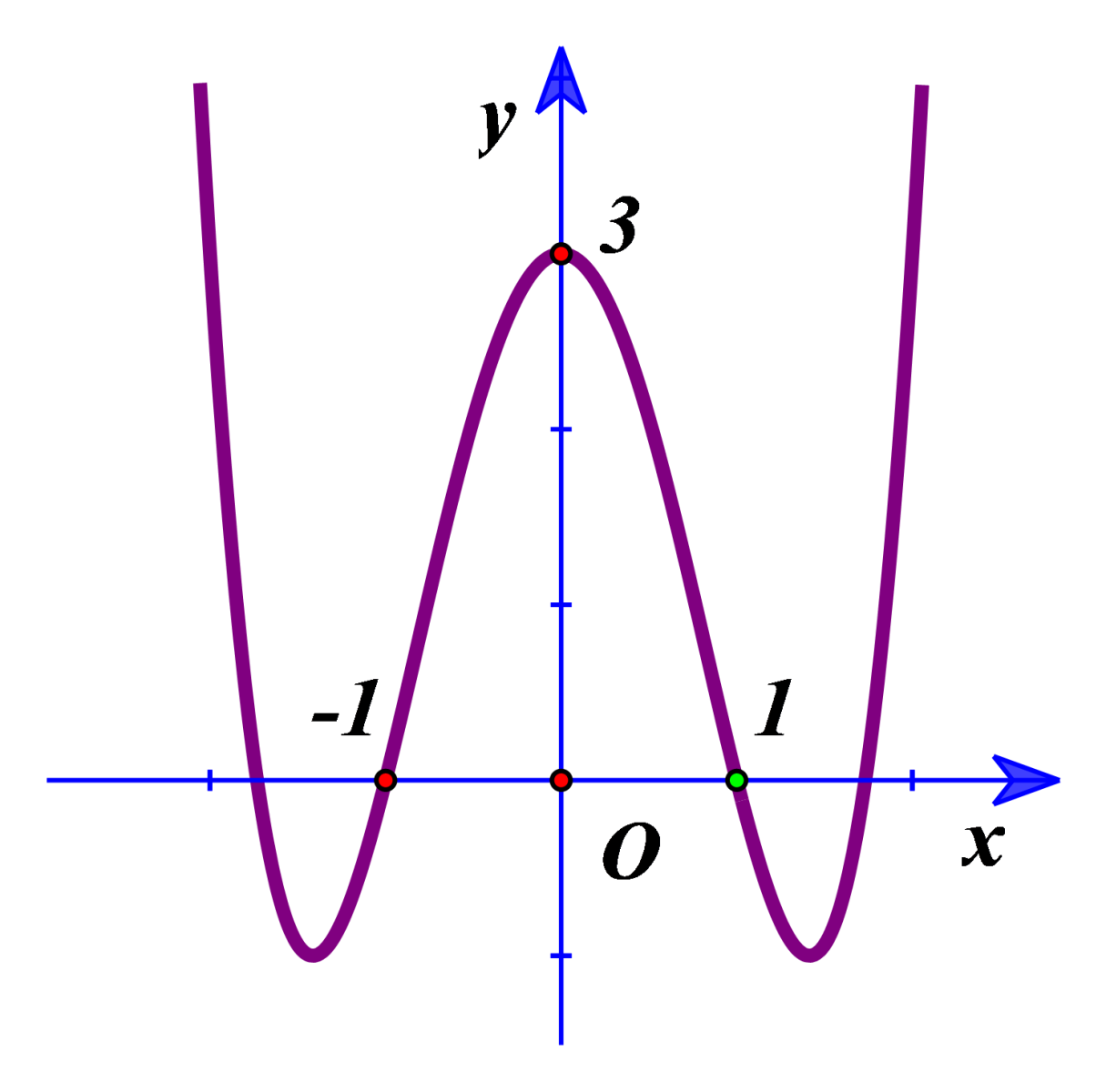
Cho hàm số $y={{x}^{3}}-3x+2$ có đồ thị như hình vẽ bên. Tìm tất cả các giá trị thực của tham số $m$ để phương trình ${{x}^{3}}-3x+2-2m=0$ có ba nghiệm thực phân biệt.
Họ nguyên hàm của hàm số $f\left( x \right)=x.\sin 2x$ là
Cho hình chóp $S.ABC$có đáy $ABC$ là tam giác đều cạnh $a$, cạnh $SA$ vuông góc với mặt phẳng đáy và $SA=2a$, gọi $M$ là trung điểm của $SC$. Tính côsin của góc $\alpha $là góc giữa đường thẳng $BM$ và $\left( ABC \right)$.
Tổng tất cả các nghiệm của phương trình ${{\log }_{2}}\left| {{x}^{2}}+2x-3 \right|-{{\log }_{2}}\left| x+3 \right|=3$ bằng
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông tại $A$, $\left( SAC \right)\bot \left( ABC \right)$, $AB=3a,\text{ }BC=5a$. Biết rằng $SA=2a\sqrt{3}$ và $\widehat{SAC}=30{}^\circ $. Khoảng cách từ điểm $A$ đến mặt phẳng $\left( SBC \right)$ bằng:
Cho $\int\limits_{1}^{3}{\frac{\ln x}{{{\left( x+1 \right)}^{2}}}\text{dx}}=\frac{a}{b}\ln 3-c\ln 2$ với $a,\text{ }b,\text{ }c\in \mathbb{N}*$ và phân số $\frac{a}{b}$ tối giản. Giá trị của $a+b+c$ bằng:
Trong không gian $Oxyz$, cho tam giác $ABC$ với $A\left( 3;-1;2 \right)$, $B\left( -1;3;5 \right)$, $C\left( 3;1;-3 \right)$. Đường trung tuyến $AM$ của $\Delta ABC$ có phương trình là
Cho số phức $z$ thỏa mãn $\left( 1-i \right)\overline{z}=5+i$. Số phức $\text{w}=2z+i$ là
Biết $\int\limits_{-1}^{2}{f\left( x \right)}\text{d}x=2$ và $\int\limits_{1}^{2}{f\left( x \right)}\text{d}x=5$, tích phân $\int\limits_{1}^{2}{f\left( 3-2x \right)}\text{d}x$ bằng
Tại SEA Games 2019, môn bóng chuyền nam có 8 đội bóng tham dự, trong đó có hai đôi Việt Nam và Thái Lan. Các đội bóng được chia ngẫu nhiên thành 2 bảng có số đội bóng bằng nhau. Xác suất để hai đội Việt Nam và Thái Lan nằm hai bảng khác nhau bằng
Một hình nón có thiết diện qua trục là một tam giác cân có góc ở đỉnh bằng ${{120}^{0}}$, cạnh bên bằng $2$. Chiều cao $h$ của hình nón là
Một vật chuyển động chậm dần đều với vận tốc $v(t)=180-20t\,\left( m/s \right)$. Tính quãng đường mà vật di chuyển được từ thời điểm $t=0\,(~s\,)$ đến thời điểm mà vật dừng lại.
Tập hợp tất cả các giá trị thực của tham số $m$ để hàm số $y={{x}^{3}}-3m{{x}^{2}}+3x-6{{m}^{3}}$ đồng biến trên khoảng $\left( 0;\text{ }+\infty \right)$ là:
Trong không gian $Oxyz$, cho điểm $M\left( 2;1;1 \right)$, mặt phẳng $\left( \alpha \right):x+y+z-4=0$ và mặt cầu $\left( S \right):{{\left( x-3 \right)}^{2}}+{{\left( y-3 \right)}^{2}}+{{\left( z-4 \right)}^{2}}=16$. Phương trình đường thẳng $\Delta $ đi qua $M$ và nằm trong $\left( \alpha \right)$ cắt mặt cầu $\left( S \right)$ theo một đoạn thẳng có độ dài nhỏ nhất. Đường thẳng $\Delta $ đi qua điểm nào trong các điểm sau đây?
Cho hình lập phương $ABCD.{A}'{B}'{C}'{D}'$ cạnh bằng 1. Gọi $M$ là trung điểm cạnh $B{B}'$. Mặt phẳng $\left( M{A}'D \right)$ cắt cạnh $BC$ tại $K$. Thể tích của khối đa điện ${A}'{B}'{C}'{D}'MKCD$ bằng:
Có bao nhiêu số phức $z$ thỏa mãn $3\left| z+\overline{z} \right|+2\left| z-\overline{z} \right|=12$ và $\left| z+2-3i \right|=\left| \overline{z}-4+i \right|$?
:
Cho hàm số $y=f\left( x \right)$ liên tục trên $\mathbb{R}$ và có đồ thị như hình vẽ bên dưới:
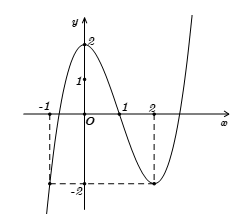
Tập hợp tất cả giá trị thực của tham số $m$ để phương trình $f\left( 2\sin x+1 \right)=m$ có nghiệm thuộc nửa khoảng $\left[ 0\,;\frac{\pi }{6} \right)$ là
Trong không gian $Oxyz$, cho hình lập phương $ABCD.{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}$ biết $A\left( 0\,;0\,;0 \right)$, $B\left( 1\,;0\,;0 \right)$, $D\left( 0\,;1\,;0 \right)$, ${{A}_{1}}\left( 0\,;0\,;1 \right)$.Gọi $\left( P \right)\text{:}\,\,ax+by+cz-3=0$ là phương trình mặt phẳng chứa $C{{D}_{1}}$ và tạo với mặt phẳng $\left( B{{B}_{1}}{{D}_{1}}D \right)$ một góc có số đo nhỏ nhất. Giá trị của $T=a+b+c$ bằng
:
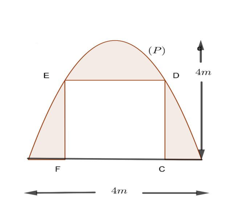
Một chiếc cổng có dạng là một parabol $\left( P \right)$ có kích thước như hình vẽ, biết chiều cao cổng bằng $4\,m\,,\,AB\,=\,4\,m$. Người ta thiết kế cửa đi là một hình chữ nhật $CDEF\,$, phần còn lại dùng để trang trí. Biết chi phí phần tô đậm là 1.000.000 đồng/${{m}^{2}}$. Hỏi số tiền ít nhất dùng để trang trí phần tô đậm gần với số tiền nào dưới đây?
Trong không gian $Oxyz$, cho $A\left( 0\,;\,1\,;\,1 \right)$, $B\left( 2\,;\,-1\,;\,1 \right)$, $C\left( 4\,;\,1\,;\,1 \right)$ và $\left( P \right)\,:\,x+\,y+z-6\,=\,0$. Xét điểm $M\left( a\,;\,b\,;\,c \right)$ thuộc $\left( P \right)$ sao cho $\left| \overrightarrow{MA}+2\overrightarrow{MB}+\overrightarrow{MC} \right|$ đạt giá trị nhỏ nhất. Giá trị của $\,2a+4b+c$ bằng:
:
Cho hàm số $f\left( x \right)$ có bảng xét dấu đạo hàm như hình bên. Hàm số $y={{e}^{3f\left( 2-x \right)+1}}+{{3}^{f\left( 2-x \right)}}$ đồng biến trên khoảng nào dưới đây?
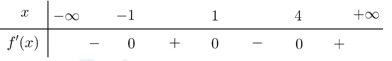
Gọi $S$ là tập hợp tất cả các giá trị nguyên dương của tham số $m$ để bất phương trình ${{x}^{6}}+3{{x}^{4}}-{{m}^{3}}{{x}^{3}}+4{{x}^{2}}-mx+2\ge 0$ đúng với mọi $x\in \left[ 1;3 \right]$. Tổng của tất cả các phần tử thuộc $S$ bằng:
Cho số phức $z=a+bi$ $\left( a,\,b\,\in \mathbb{R} \right)$ thỏa mãn $\left| z+4 \right|+\left| z-4 \right|=10$ và $\left| z-6 \right|$ lớn nhất. Tính $S=a+b$.
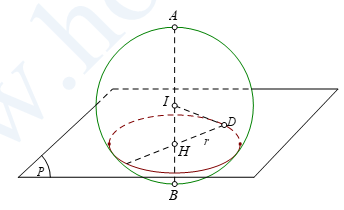
Trong không gian với hệ trục tọa độ $Oxyz,$cho hai điểm $A\left( 2;1;3 \right),B\left( 6;5;5 \right)$. Gọi $\left( S \right)$ là mặt cầu đường kính $AB$. Mặt phẳng $\left( P \right)$ vuông góc với $AB$ tại $H$ sao cho khối nón đỉnh $A$ và đáy là hình tròn tâm $H$ là giao tuyến của $\left( S \right)$ và $\left( P \right)$ có thể tích lớn nhất, biết rằng $\left( P \right):2x+by+cz+d=0$ với $b,c,d\in \mathbb{Z}$. Tính $S=b+c+d.$
Cho hàm số $f\left( x \right)$ có đạo hàm liên tục trên đoạn $\left[ 1\,;2 \right]$ thỏa mãn $\int\limits_{1}^{2}{{{\left( x-1 \right)}^{2}}f\left( x \right)\text{d}x}=-\frac{1}{3}$, $f\left( 2 \right)=0$ và $\int\limits_{1}^{2}{{{\left[ {f}'\left( x \right) \right]}^{2}}\text{d}x}=7$. Tính tích phân $I=\int\limits_{1}^{2}{f\left( x \right)\text{d}x}$.
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh bằng 1. Biết khoảng cách từ $A$ đến mặt phẳng $\left( SBC \right)$ là $\frac{\sqrt{6}}{4}$, từ $B$ đến mặt phẳng $\left( SAC \right)$ là $\frac{\sqrt{15}}{10}$, từ $C$ đến mặt phẳng $\left( SAB \right)$ là $\frac{\sqrt{30}}{20}$.và hình chiếu vuông góc của $S$ xuống đáy nằm trong tam giác $ABC$. Thể tích khối chóp $S.ABC$ bằng
Cho phương trình ${{3}^{x}}\left( {{3}^{2x}}+1 \right)-\left( {{3}^{x}}+m+2 \right)\sqrt{{{3}^{x}}+m+3}=2\sqrt{{{3}^{x}}+m+3}$, với $m$ là tham số. Có bao nhiêu giá trị nguyên âm của $m$ để phương trình có nghiệm thực?



.PNG)
.PNG)
.PNG)
.PNG)
.PNG)



.PNG)
.PNG)
.PNG)
