Đề thi thử tốt nghiệp THPT môn Toán năm 2023 online - Đề thi của Trường THPT Bà Điểm
Vui lòng cài đặt đề thi trước khi làm bài
Cho số phức $z=-4+5i$. Biểu diễn hình học của $z$ là điểm có tọa độ
Trên khoảng $\left( 0;+\infty \right)$, đạo hàm của hàm số$y={{\log }_{2}}x$ là:
Trên khoảng $\left( 0;+\infty \right)$, đạo hàm của hàm số $y={{x}^{e}}$ là
Tập nghiệm của bất phương trình ${{2}^{x+1}}>8$ là
Cho cấp số cộng $\left( {{u}_{n}} \right)$ có ${{u}_{1}}=3$ và ${{u}_{2}}=-1$. Công sai của cấp số cộng đó bằng
Trong không gian $Oxyz$, cho 3 điểm $M\left( 2;1;-3 \right)$, $N\left( 1;0;2 \right)$; $P\left( 2;-3;5 \right)$. Tìm một vectơ pháp tuyến $\overrightarrow{n}$ của mặt phẳng $\left( MNP \right)$.
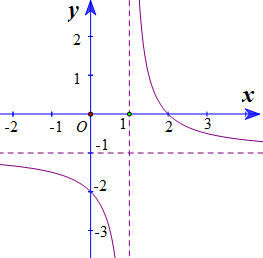
Cho hàm số $y=\frac{ax+b}{cx+d}$ có đồ thị là đường cong trong hình vẽ bên. Tọa độ giao điểm của đồ thị hàm số đã cho và trục hoành là
Biết $\int\limits_{1}^{2}{f\left( x \right)\text{d}x=6}$, $\int\limits_{2}^{5}{f\left( x \right)\text{d}x=1}$, tính $I=\int\limits_{1}^{5}{f\left( x \right)\text{d}x}$.
:
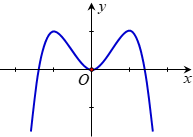
Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên?
Trong không gian $Oxyz$, cho mặt cầu $\left( S \right):{{x}^{2}}+{{y}^{2}}+{{z}^{2}}-2y+4z-2=0$. Bán kính mặt cầu bằng
Trong không gian $Oxy$, góc giữa hai trục $Ox$ và $Oz$ bằng
Cho số phức $z=3+5i$, phần ảo của số phức ${{\bar{z}}^{2}}$ bằng
Cho khối lăng trụ đứng có chiều cao bằng $3$ và đáy là tam giác đều có độ dài cạnh bằng 2. Tính thể tích khối lăng trụ đã cho
Cho khối chóp $S.ABC$ có đáy là tam giác vuông tại $B.$ Biết $BC=a\sqrt{3}\,,\ AB=a$, $SA$ vuông góc với đáy, $SA=2a\sqrt{3}$. Thể tích khối chóp $S.ABC$ bằng
.png)
Trong không gian $Oxyz$, cho hai mặt cầu $\left( S \right):\,\,{{\left( x-3 \right)}^{2}}+{{y}^{2}}+{{z}^{2}}=9$ và $\left( S' \right):\,\,{{\left( x+2 \right)}^{2}}+{{y}^{2}}+{{z}^{2}}=4$. Khẳng định nào sau đây là đúng?
Phần thực của số phức $z=4-2i$ bằng
Diện tích xung quanh của hình nón có bán kính đáy $r=5cm$và độ dài đường sinh $l=7cm$ bằng
Trong không gian với hệ trục tọa độ $Oxyz$, cho mặt phẳng $\left( P \right)$ có phương trình $x+2y-3z-2=0$. Điểm nào sau đây thuộc mặt phẳng $\left( P \right)$?
:
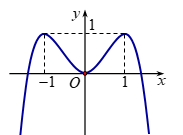
Cho hàm số $y=a x^4+b x^2+c$ có đồ thị là đường cong trong hình bên. Điểm cực tiểu của đồ thị hàm số đã cho có tọa độ là
Tiệm cận đứng của đồ thị hàm số $y=\frac{x-1}{x-3}$ là đường thẳng có phương trình
Tập nghiệm của bất phương trình $lo{{g}_{2}}\left( x+1 \right)<3$ là
Cho tập hợp $M=\left\{ 1;2;3;4;5 \right\}$. Số tập con gồm hai phần tử của tập hợp $M$ là:
Cho $\int{\cos 3x.dx}=F\left( x \right)+C$. Khẳng định nào dưới đây đúng?
Cho $\int\limits_{2}^{4}{f\left( x \right)\text{d}x}=10$. Tính $I=\int\limits_{2}^{4}{\left[ 3f\left( x \right)-5 \right]\text{d}x}$
Họ tất cả các nguyên hàm của hàm số $f\left( x \right)=3{{x}^{2}}-2\cos x$ là
:
Cho hàm số bậc ba $y=f\left( x \right)$ có đồ thị như hình sau
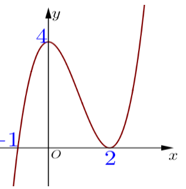
Hàm số $y=f\left( x \right)$ nghịch biến trên khoảng nào dưới đây?
Cho hàm số $y=f(x)$ có bảng biến thiên như sau
Giá trị cực đại của hàm số đã cho là
Kết quả thu gọn biểu thức $P=\ln \left( 4x \right)-\ln \left( 2x \right)$ là
Giả sử $D$ là hình phẳng giới hạn bởi đường parabol $y={{x}^{2}}-3x+2$ và trục hoành. Quay $D$ quanh trục hoành ta thu được khối tròn xoay có thể tích bằng
Cho hình hộp chữ nhật $ABCD.A'B'C'D'$, $BC=a,\ AC=2a,\ {A}'A=a\sqrt{3}$. Tính góc giữa mặt phẳng $\left( BCD'A' \right)$ và mặt phẳng $\left( ABCD \right)$.
Cho hàm số bậc ba $y=f\left( x \right)$ có đồ thị là đường cong trong hình bên.
Có bao nhiêu giá trị nguyên của tham số $m$ để phương trình $f\left( x \right)+1=m$ có hai nghiệm không âm?
:
Cho hàm số bậc bốn $y=f\left( x \right)$. Hàm số $y={f}'\left( x \right)$ có đồ thị như hình vẽ sau
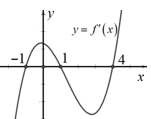
Hàm số $y=f\left( x \right)$ nghịch biến trên khoảng nào trong các khoảng sau?
Thầy Bình đặt lên bàn $30$ tấm thẻ đánh số từ $1$ đến $30$. Bạn An chọn ngẫu nhiên $10$ tấm thẻ. Tính xác suất để trong $10$ tấm thẻ lấy ra có $5$ tấm thẻ mang số lẻ, $5$ tấm mang số chẵn trong đó chỉ có một tấm thẻ mang số chia hết cho $10$.
Tích các nghiệm của phương trình$\log _{2}^{2}x-3{{\log }_{2}}x+2=0$là
Tập hợp các điểm biểu diễn số phức $z$ thỏa mãn $\left| z-i \right|=\left| \left( 1+i \right)z \right|$ là một đường tròn, tâm của đường tròn đó có tọa độ là
Trong không gian $Oxyz$, cho ba điểm $A\left( 3\,;-1\,\,;2 \right)$, $B\left( 0\,;\,1\,;\,3 \right)$ và $C\left( -1;\,1\,;1 \right)$. Đường thẳng đi qua $C$ và song song với đường thẳng $AB$ có phương trình là:
Trong không gian với hệ tọa độ $Oxyz$, cho ba điểm $A\left( 2;\,0;\,-1 \right)$, $B\left( 1;\,-2;\,3 \right)$, $C\left( 0;\,1;\,2 \right)$. Tìm tọa độ điểm ${O}'$ là điểm đối xứng với gốc tọa độ $O$ qua mặt phẳng $\left( ABC \right)$.
Cho hình chóp $S.ABC$ có đáy là tam giác vuông tại $B$, $AB=a$, $AC=3a$ và $SA$ vuông góc với mặt phẳng đáy. Khoảng cách từ $C$ đến mặt phẳng $\left( SAB \right)$ bằng
Có bao nhiêu số nguyên $x$ thỏa mãn $\text{lo}{{\text{g}}_{3}}\frac{{{x}^{2}}-9}{125}\le \text{lo}{{\text{g}}_{5}}\frac{{{x}^{2}}-9}{27}$?
Cho hàm số $f\left( x \right)$ liên tục trên $\mathbb{R}$. Gọi $F\left( x \right),G\left( x \right),H\left( x \right)$ là ba nguyên hàm của $f\left( x \right)$ trên $\mathbb{R}$ thỏa mãn $F\left( 8 \right)+G\left( 8 \right)+H\left( 8 \right)=4$ và $F\left( 0 \right)+G\left( 0 \right)+H\left( 0 \right)=1$. Khi đó $\int\limits_{0}^{2}{f}\left( 4x \right)\text{d}x$ bằng
Tìm tất cả các giá trị thực của tham số $m$ sao cho đồ thị hàm số
$y={{x}^{4}}-2m{{x}^{2}}+2{{m}^{4}}-m$ có ba điểm cực trị đều thuộc các trục toạ độ
Xét các số phức $z,$ $\text{w}$ thỏa mãn $\left| z \right|=2$ và $\left| i.\overline{w} \right|=1$. Khi $\left| iz+w+3-4i \right|$ đạt giá trị nhỏ nhất, $\left| z-\text{w} \right|$ bằng
Cho hình lăng trụ đứng $ABC.{A}'{B}'{C}'$ có đáy là tam giác vuông cân đỉnh $A$, mặt bên là $BC{C}'{B}'$ hình vuông, khoảng cách giữa $A{B}'$ và $C{C}'$ bằng $a$. Thể tích khối lăng trụ $ABC.{A}'{B}'{C}'$ là
Cho hàm số $f\left( x \right)$ có đạo hàm liên tục trên $\mathbb{R}$ thỏa mãn $f\left( 0 \right)=0$ và ${f}'\left( x \right)\left( 1+{{e}^{f\left( x \right)}} \right)=1+{{e}^{x}},\forall x\in \mathbb{R}.$ Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số $y=f\left( x \right)$, trục hoành và hai đường thẳng $x=1,x=3.$
Có bao nhiêu giá trị nguyên của tham số $m$để trên tập số phức, phương trình ${{z}^{2}}+2mz+{{m}^{2}}-m-2=0$ có hai nghiệm ${{z}_{1}},\text{ }{{z}_{2}}$ thoả mãn $\left| {{z}_{1}} \right|\text{+}\left| \text{ }{{z}_{2}} \right|=2\sqrt{10}$.
Trong không gian $Oxyz$, cho điểm $M\left( 1;0;-2 \right)$ và đường thẳng $d:\left\{ \begin{align} & x=1-2t \\ & y=t \\ & z=-1-t \\\end{align} \right.$. Gọi $\left( P \right)$ là mặt phẳng đi qua $M$ và chứa $d$. Tổng khoảng cách từ điểm $N\left( -3;-2;1 \right)$ và $Q\left( -1;3;0 \right)$ đến $\left( P \right)$ bằng
Có bao nhiêu cặp số nguyên$(x,y)$ thỏa mãn ${{2}^{{{x}^{2}}+{{y}^{2}}+1}}\le \left( {{x}^{2}}+{{y}^{2}}-2x+2 \right){{.4}^{x}}$.
Cho hình trụ có bán kính $R$ và chiều cao $\sqrt{3}R$. Hai điểm $A$, $B$ lần lượt nằm trên hai đường tròn đáy sao cho góc giữa $AB$ và trục $d$ của hình trụ bằng $30{}^\circ $. Tính khoảng cách giữa $AB$ và trục của hình trụ.
Trong không gian $Oxyz,$ cho $A\left( 0;0;1 \right),B\left( 0;0;9 \right),Q\left( 3;4;6 \right)$. Xét các điểm $M$ thay đổi sao cho tam giác $ABM$ vuông tại $M$ và có diện tích lớn nhất. Giá trị nhỏ nhất của độ dài đoạn thẳng $MQ$ thuộc khoảng nào dưới đây?
Có bao nhiêu giá trị nguyên âm của tham số $m$ để hàm số$y=\left| {{x}^{5}}+2{{x}^{4}}-m{{x}^{2}}+3x-20 \right|$ nghịch biến trên $\left( -\infty ;-2 \right)$?


.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
