Đề thi thử THPT QG năm 2022 môn Toán online - Đề thi của Trường THPT Thanh Đa
Vui lòng cài đặt đề thi trước khi làm bài
Cho hàm số $y = \dfrac{{2x + 1}}{{x + 2}}$. Khẳng định nào dưới đây đúng?
Với $a$ là số thực dương khác $1$ tùy ý, ${\log _{{a^2}}}{a^3}$ bằng
Hàm số $y = \dfrac{1}{3}{x^3} + {x^2} - 3x + 1$ đạt cực tiểu tại điểm
Thể tích của khối chóp có diện tích đáy bằng $6$ và chiều cao bằng $4$ là
Cho hình hộp đứng $ABCD.A'B'C'D'$ có đáy $ABCD$ là hình thoi có hai đường chéo $AC = a$, $BD = a\sqrt 3 $ và cạnh bên $AA' = a\sqrt 2 $. Thể tích $V$ của khối hộp đã cho là
Cho hàm số $y = a{x^3} + b{x^2} + cx + d$ $\left( {a \ne 0} \right)$ có đồ thị như hình dưới đây.
Khẳng định nào dưới đây đúng?
:
Cho hàm số $y = f\left( x \right)$ có bảng xét dấu của đạo hàm như sau.
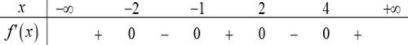
Hàm số $y = - 2f\left( x \right) + 2019$ nghịch biến trên khoảng nào trong các khoảng dưới đây?
Cho $a$ và $b$ lần lượt là số hạng thứ hai và thứ mười của một cấp số cộng có công sai $d \ne 0.$ Giá trị của biểu thức ${\log _2}\left( {\dfrac{{b - a}}{d}} \right)$ là một số nguyên có số ước tự nhiên bằng
Cho khối chóp tứ giác $S.ABCD$có đáy $ABCD$ là hình thoi và $SABC$ là tứ diện đều cạnh $a$. Thể tích $V$ của khối chóp $S.ABCD$ là
Cho khối chóp tam giác $S.ABC$ có đỉnh $S$ và đáy là tam giác $ABC$. Gọi $V$ là thể tích của khối chóp. Mặt phẳng đi qua trọng tâm của ba mặt bên của khối chóp chia khối chóp thành hai phần. Tính theo $V$ thể tích của phần chứa đáy của khối chóp.
Cho mặt cầu $\left( S \right)$ tâm $O$, bán kính bằng 2. $\left( P \right)$ là mặt phẳng cách $O$ một khoảng bằng 1 và cắt $\left( S \right)$ theo một đường tròn $\left( C \right)$. Hình nón $\left( N \right)$ có đáy là $\left( C \right)$, đỉnh thuộc $\left( S \right)$, đỉnh cách $\left( P \right)$ một khoảng lớn hơn $2$. Kí hiệu ${V_1}$, ${V_2}$ lần lượt là thể tích của khối cầu $\left( S \right)$ và khối nón $\left( N \right)$. Tỉ số $\dfrac{{{V_1}}}{{{V_2}}}$ là
Tìm tất cả các giá trị thực của tham số $m$ để phương trình ${x^3} - 3mx + 2 = 0$ có nghiệm duy nhất.
Cho hình chóp $S.ABC$ có tam giác $ABC$ vuông tại $B$, $\widehat C = 60^\circ $, $AC = 2$, $SA \bot \left( {ABC} \right)$, $SA = 1$. Gọi $M$ là trung điểm của $AB$. Khoảng cách $d$ giữa $SM$ và $BC$ là
Gọi $M$ và $m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = \dfrac{{3\cos x - 1}}{{3 + \cos x}}$. Tổng $M + m$ là
Cho hàm số $y = a{x^4} + b{x^2} + c$ ($a \ne 0$) có đồ thị như hình vẽ dưới đây.
Mệnh đề nào dưới đây đúng?
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật, $AB = AD\sqrt 2 $, $SA \bot \left( {ABC} \right)$. Gọi $M$ là trung điểm của $AB$. Góc giữa hai mặt phẳng $\left( {SAC} \right)$ và $\left( {SDM} \right)$ bằng
Trong mặt phẳng với hệ tọa độ $Oxy$, cho hai đường tròn $\left( {{C_1}} \right)$ và $\left( {{C_2}} \right)$ lần lượt có phương trình ${\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} = 1$ và ${\left( {x + 1} \right)^2} + {y^2} = 1$. Biết đồ thị hàm số $y = \dfrac{{ax + b}}{{x + c}}$ đi qua tâm của $\left( {{C_1}} \right)$, đi qua tâm của $\left( {{C_2}} \right)$ và có các đường tiệm cận tiếp xúc với cả $\left( {{C_1}} \right)$ và $\left( {{C_2}} \right)$. Tổng $a + b + c$ là
:
Cho hàm số $y = f\left( x \right)$ có đồ thị như hình dưới đây.
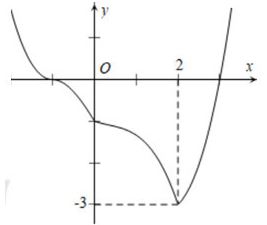
Tìm tất cả các giá trị thực của tham số $m$ để bất phương trình $2f\left( x \right) + {x^2} > 4x + m$ nghiệm đúng với mọi $x \in \left( { - 1;3} \right)$.
Cho $x \in \left( {0;\dfrac{\pi }{2}} \right)$. Biết $\log \sin x + \log \cos x = - 1$ và $\log \left( {\sin x + \cos x} \right) = \dfrac{1}{2}\left( {\log n - 1} \right)$. Giá trị của $n$ là
Cho tứ diện $ABCD$. Trên các cạnh $AB$,$BC$, $CA$, $AD$ lần lượt lấy 3; 4; 5; 6 điểm phân biệt khác các điểm $A$, $B$, $C$, $D$. Số tam giác phân biệt có các đỉnh là các điểm vừa lấy là
Cho hình chóp đều $S.ABC$ có độ dài cạnh đáy bằng $2$, điểm $M$ thuộc cạnh $SA$ sao cho $SA = 4SM$ và $SA$ vuông góc với mặt phẳng $\left( {MBC} \right)$. Thể tích $V$ của khối chóp $S.ABC$ là
Cho hình trụ có hai đáy là hai hình tròn $\left( {O;R} \right)$ và $\left( {O';R} \right)$. $AB$ là một dây cung của đường tròn $\left( {O;R} \right)$ sao cho tam giác $O'AB$ là tam giác đều và mặt phẳng $\left( {O'AB} \right)$ tạo với mặt phẳng chứa đường tròn $\left( {O;R} \right)$ một góc $60^\circ $. Tính theo $R$ thể tích $V$ của khối trụ đã cho.
Biết ${\log _2}\left( {\sum\limits_{k = 1}^{100} {\left( {k \times {2^k}} \right)} - 2} \right) = a + {\log _c}b$ với $a$,$b$,$c$ là các số nguyên và $a > b > c > 1$. Tổng $a + b + c$ là
Số giá trị nguyên của tham số $m$ nằm trong khoảng $\left( {0;2020} \right)$ để phương trình $\left| {\left| {x - 1} \right| - \left| {2019 - x} \right|} \right| = 2020 - m$ có nghiệm là
Một cái hộp có dạng hình hộp chữ nhật có thể tích bằng $48$ và chiều dài gấp đôi chiều rộng. Chất liệu làm đáy và 4 mặt bên của hộp có giá thành gấp ba lần giá thành của chất liệu làm nắp hộp. Gọi $h$ là chiều cao của hộp để giá thành của hộp là thấp nhất. Biết $h = \dfrac{m}{n}$ với $m$, $n$ là các số nguyên dương nguyên tố cùng nhau. Tổng $m + n$ là
Cho hàm số $f\left( x \right) = m{x^4} + n{x^3} + p{x^2} + qx + r$ $\left( {m \ne 0} \right)$. Chia $f\left( x \right)$ cho $x - 2$ được phần dư bằng $2019$, chia $f'\left( x \right)$ cho $x - 2$ được phần dư bằng 2018. Gọi $g\left( x \right)$ là phần dư khi chia $f\left( x \right)$ cho ${\left( {x - 2} \right)^2}$. Giá trị của $g\left( { - 1} \right)$ là
Cho hình chóp tứ giác đều $S.ABCD$ có cạnh đáy bằng $a$, cạnh bên bằng $\sqrt 2 a$. Độ lớn của góc giữa đường thẳng $SA$ và mặt phẳng đáy bằng:
:
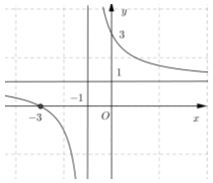
Hình vẽ là đồ thị của hàm số:
Đường thẳng $\left( \Delta \right)$ là giao của hai mặt phẳng $x + z - 5 = 0$ và $x - 2y - z + 3 = 0$ thì có phương trình là:
Mặt phẳng $\left( P \right)$ đi qua $A\left( {3;0;0} \right),\,\,B\left( {0;0;4} \right)$ và song song trục $Oy$ có phương trình:
Cho lăng trụ đều $ABC.A'B'C'$ có $AB = 2\sqrt 3 ,\,\,BB' = 2$.Gọi $M,\,\,N,\,\,P$ tương ứng là trung điểm của $A'B',\,\,A'C',\,\,BC$. Nếu gọi $\alpha $ là độ lớn của góc của hai mặt phẳng $\left( {MNP} \right)$ và $\left( {ACC'} \right)$ thì $\cos \alpha $ bằng:
Lăng trụ có chiều cao bằng $a$, đáy là tam giác vuông cân và có thể tích bằng $2{a^3}$. Cạnh góc vuông của đáy lăng trụ bằng
Tổng các nghiệm của phương trình ${4^x} - {6.2^x} + 2 = 0$ bằng:
Xét các số phức $z$ thỏa mãn $\left| {z - 1 - 3i} \right| = 2$. Số phức $z$ mà $\left| {z - 1} \right|$ nhỏ nhất là:
Cho hàm số $f\left( x \right) = \left\{ \begin{array}{l}{e^x} + m\,\,\,khi\,\,x \ge 0\\2x\sqrt {3 + {x^2}} \,\,khi\,\,x < 0\end{array} \right.$ liên tục trên và $\int\limits_{ - 1}^1 {f\left( x \right)dx} = ae + b\sqrt 3 + c$, $\left( {a,b,c \in \mathbb{Q}} \right)$. Tổng $T = a + b + 3c$ bằng:
Cho hình chóp đều $S.ABCD$ có cạnh đáy bằng $2$và cạnh bên bằng $2\sqrt 2 $. Gọi $\alpha $là góc của mặt phẳng $\left( {SAC} \right)$ và mặt phẳng $\left( {SAB} \right)$. Khi đó $\cos \alpha $ bằng:
Trong không gian $Oxyz$, cho $A\left( {2;0;0} \right),\,\,B\left( {0;4;0} \right),\,\,C\left( {0;0;6} \right),\,\,D\left( {2;4;6} \right)$. Gọi $\left( P \right)$ là mặt phẳng song song với $mp\left( {ABC} \right)$, $\left( P \right)$ cách đều $D$ và mặt phẳng $\left( {ABC} \right)$. Phương trình của $\left( P \right)$ là:
Số nào sau đây là điểm cực đại của hàm số $y = {x^4} - 2{x^3} + {x^2} + 2$?
Cho hàm số $f\left( x \right)$ có đạo hàm liên tục trên $\mathbb{R}$, $f\left( 0 \right) = 0,\,\,f'\left( 0 \right) \ne 0$ và thỏa mãn hệ thức$f\left( x \right)/f'\left( x \right) + 18{x^2} = \left( {3{x^2} + x} \right)f'\left( x \right) + \left( {6x + 1} \right)f\left( x \right)\,\,\forall x \in \mathbb{R}$. Biết $\int\limits_0^1 {\left( {x + 1} \right){e^{f\left( x \right)}}dx} = a{e^2} + b\,\,\left( {a,\,\,b \in \mathbb{Q}} \right)$. Giá trị của $a - b$ bằng:
Hàm số $y = - {x^3} + 3{x^2} - 2$ đồng biến trên khoảng:
Cho hàm số $f\left( x \right)$ liên tục trên $\mathbb{R}$ và $\int\limits_0^4 {f\left( x \right)dx} = 10,\,\,\int\limits_3^4 {f\left( x \right)dx} = 4$. Tích phân $\int\limits_0^3 {f\left( x \right)dx} $ bằng:
Một hộp có 10 quả cầu xanh, 5 quả cầu đỏ. Lấy ngẫu nhiên 5 quả từ hộp đó. Xác suất để được 5 quả có đủ hai màu là:
Tập xác định của hàm số $y = {\left[ {\ln \left( {x - 2} \right)} \right]^\pi }$ là:
Cho hình hộp chữ nhật $ABCD.A'B'C'D'$ có $AB = a,\,\,AD = AA' = 2a$. Khoảng cách giữa hai đường thẳng $AC$ và $DC'$ bằng:
Hàm số $y = f\left( x \right)$ có đạo hàm liên tục trên $\mathbb{R}$ và dấu của đạo hàm được cho bởi bảng dưới đây:
Hàm số $y = f\left( {2x - 2} \right)$ nghịch biến trên khoảng:
Cho $n \in {\mathbb{N}^*}$ và $C_n^2.C_n^{n - 2} + C_n^8.C_n^{n - 8} = 2C_n^2.C_n^{n - 8}$ . Tổng $T = {1^2}C_n^1 + {2^2}C_n^2 + ... + {n^2}C_n^n$ bằng:
Cho $n \in \mathbb{N}$ và $n! = 1$. Số giá trị của $n$ thỏa mãn giả thiết đã cho là:
:
Cho hàm số có đồ thị như hình dưới đây. Hàm số $g\left( x \right) = \ln \left( {f\left( x \right)} \right)$ đồng biến trên khoảng nào dưới đây?
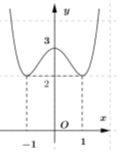
Cần sản xuất một vỏ hộp sữa hình trụ có thể tích $V$ cho trước. Để tiết kiệm vật liệu nhất thì bán kính đáy phải bằng
Bất phương trình ${4^x} - \left( {m + 1} \right){2^{x + 1}} + m \ge 0$ nghiệm đúng với mọi $x \ge 0$. Tập tất cả các giá trị của $m$ là:

.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
