Đề thi thử THPT QG năm 2022 môn Toán online - Đề thi của Trường THPT Ngô Gia Tự
Vui lòng cài đặt đề thi trước khi làm bài
Họ nguyên hàm của hàm số $f\left( x \right) = {x^2} + 3$ là:
Tích phân $\int\limits_0^1 {\dfrac{1}{{2x + 5}}dx} $ bằng
Cho số phức $z = 2 + 5i$. Điểm biểu diễn số phức z trong mặt phẳng Oxy có tọa độ là:
Trong không gian Oxyz, phương trình tham số của đường thẳng đi qua điểm $M\left( {2;0; - 1} \right)$ và có vectơ chỉ phương $\overrightarrow u = \left( {2; - 3;1} \right)$ là:
Trong không gian Oxyz, cho $\overrightarrow a = \left( {1;2;3} \right),\,\overrightarrow b = \left( {4;5;6} \right)$. Tọa độ $\overrightarrow a + \overrightarrow b $ là:
Trong không gian Oxyz, cho mặt phẳng $\left( P \right):x + y - 2z + 4 = 0$. Một vectơ pháp tuyến của mặt phẳng (P) là:
:
Cho hàm số $y = f\left( x \right)$ liên tục trên $\mathbb{R}$ có bảng biến thiên như hình vẽ. Khẳng định nào sau đây đúng?
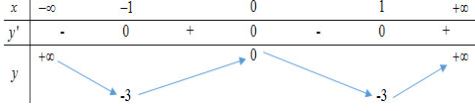
:
Cho hàm số $f\left( x \right)$ có đồ thị hàm số như hình vẽ. Khẳng định nào sai?
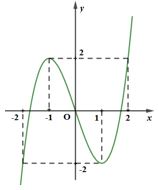
Phương trình ${\log _2}\left( {x + 1} \right) = 2$ có nghiệm là:
Đồ thị hàm số nào đi qua điểm $M\left( {1;2} \right)$:
Cho một cấp số cộng $\left( {{u_n}} \right)$ có ${u_1} = \dfrac{1}{2}$, ${u_2} = \dfrac{7}{2}$. Khi đó công sai d bằng:
Trong các hàm số sau đây, hàm số nào đồng biến trên $\mathbb{R}$
Thể tích của một khối lăng trụ có đường cao bằng 3a, diện tích mặt đáy bằng $4{a^2}$ là:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = a, $BC = a\sqrt 3 $. Cạnh bên SA vuông góc với đáy và đường thẳng SD tạo với mặt phẳng (ABCD) một góc ${30^0}$. Thể tích của khối chóp S.ABCD bằng:
Đạo hàm của hàm số $y = {\left( {{x^3} - 2{x^2}} \right)^2}$ bằng:
Gọi M và N là giao điểm của đồ thị hai hàm số $y = {x^4} - 2{x^2} + 2$ và $y = - {x^2} + 4$. Tọa độ trung điểm I của đoạn thẳng MN là:
Diện tích S của hình phẳng (H) giới hạn bởi hai đường cong $y = - {x^3} + 12x$ và $y = - {x^2}$ là:
Trong không gian Oxyz, cho hai điểm $A\left( { - 2;1;1} \right),B\left( {0; - 1;1} \right)$. Phương trình mặt cầu đường kính $AB$ là:
Cho hàm số $y = - {x^4} + 2{x^2} + 3$ có giá trị cực đại và giá trị cực tiểu lần lượt là ${y_1},{y_2}$. Khi đó: ${y_1} + {y_2}$ bằng
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với $AB = a,\,BC = a\sqrt 3 $, cạnh $SA = 2a$, $SA$ vuông góc với mặt phẳng (ABCD). Gọi $\alpha $ là góc giữa đường thẳng SC và mặt phẳng (ABCD). Giá trị $\tan \alpha $ bằng:
Cho số phức z thỏa mãn $\left( {1 + 2i} \right)z = 6 - 3i$. Phần thực của số phức z là:
Tập nghiệm S của bất phương trình ${\log _{\dfrac{1}{2}}}\left( {{x^2} - 3x + 2} \right) \ge - 1$ là:
Trong không gian Oxyz, cho hai mặt phẳng $\left( P \right):2x - y - 2z - 9 = 0$,$\left( Q \right):x - y - 6 = 0$. Góc giữa hai mặt phẳng $\left( P \right),\left( Q \right)$ bằng:
Gọi ${z_1},{z_2}$ là hai nghiệm phức của phương trình ${z^2} - 2z + 2018 = 0$. Khi đó, giá trị của biểu thức $A = \left| {{z_1} + {z_2} - {z_1}{z_2}} \right|$ bằng:
Tọa độ giao điểm của hai đường tiệm cận của đồ thị hàm số $y = \dfrac{{3x - 7}}{{x + 2}}$ là:
Giá trị nhỏ nhất của hàm số $y = \dfrac{{x + 3}}{{2x - 3}}$ trên đoạn $\left[ {2;5} \right]$ bằng:
Cho $a = {\log _3}2;\,\,b = {\log _3}5$. Khi đó $\log 60$ bằng:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, $\widehat {ABC} = {30^0}$. SBC là tam giác đều cạnh a và mặt bên $SBC$ vuông góc với đáy. Khoảng cách từ điểm C đến mặt phẳng (SAB) là:
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, $AC = 2\sqrt 3 a,\,\,BD = 2a$, hai mặt phẳng $\left( {SAC} \right)$ và $\left( {SBD} \right)$ cùng vuông góc với mặt phẳng (ABCD). Biết khoảng cách từ điểm O đến (SAB) bằng $\dfrac{{a\sqrt 3 }}{4}$. Thể tích của khối chóp S.ABCD là:
Biết rằng trên khoảng $\left( {\dfrac{3}{2}; + \infty } \right)$, hàm số $f\left( x \right) = \dfrac{{20{x^2} - 30x + 7}}{{\sqrt {2x - 3} }}$ có một nguyên hàm $F\left( x \right) = \left( {a{x^2} + bx + c} \right)\sqrt {2x - 3} ,\,\,\left( {a,b,c \in \mathbb{Z}} \right)$. Tổng $S = a + b + c$ bằng:
Cho hàm số $f\left( x \right)$ liên tục trên $\mathbb{R}$ và $f\left( 2 \right) = 16$, $\int\limits_0^2 {f\left( x \right)dx} = 4$. Tính tích phân $I = \int\limits_0^1 {x.f'\left( {2x} \right)dx} $.
Cho hàm số $y = a{x^3} + b{x^2} + cx + d$ có đồ thị như hình vẽ bên. Mệnh đề nào sau đây đúng?
Số nghiệm của phương trình ${\left( {{{\log }_2}4x} \right)^2} - 3.{\log _{\sqrt 2 }}x - 7 = 0$ là:
Cho hàm số $y = - \dfrac{1}{3}{x^3} + m{x^2} + \left( {3m + 2} \right)x - 5$. Tập hợp tất cả các giá trị của tham số m để hàm số nghịch biến trên $\left( { - \infty ; + \infty } \right)$ là $\left[ {a;b} \right]$. Khi đó $a - 3b$ bằng
Có bao nhiêu số phức z thỏa mãn $\left| {z - 2i} \right| = \sqrt 2 $ và ${z^2}$ là số thuần ảo?
Trong không gian Oxyz, cho hai đường thẳng ${d_1}:\dfrac{{x + 1}}{3} = \dfrac{{y - 1}}{2} = \dfrac{{z - 2}}{{ - 1}}$, ${d_2}:\dfrac{{x - 1}}{{ - 1}} = \dfrac{{y - 1}}{2} = \dfrac{{z + 1}}{{ - 1}}$. Đường thẳng $\Delta $ đi qua điểm $A\left( {1;2;3} \right)$ vuông góc với ${d_1}$ và cắt đường thẳng ${d_2}$ có phương trình là:
Cho hình phẳng (H) giới hạn bởi đồ thị các hàm số sau $y = \sqrt x ,y = 1$ và đường thẳng $x = 4$ (tham khảo hình vẽ). Thể tích khối tròn xoay sinh bởi hình (H) khi quay quanh đường thẳng $y = 1$ bằng
:
Cho hàm số bậc ba $y = a{x^3} + b{x^2} + cx + d$ có đồ thị như hình vẽ bên. Hỏi đồ thị hàm số $g\left( x \right) = \dfrac{{\left( {{x^2} - 4x + 4} \right)\sqrt {x - 1} }}{{x\left[ {{f^2}\left( x \right) - f\left( x \right)} \right]}}$ có bao nhiêu đường tiệm cận đứng?
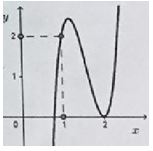
Cho hàm số $y = f\left( x \right)$, biết hàm số $f\left( x \right)$ có đạo hàm $f'\left( x \right)$ và hàm số $y = f'\left( x \right)$ có đồ thị như hình vẽ. Đặt $g\left( x \right) = f\left( {x + 1} \right)$. Kết luận nào sau đây đúng?
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B. Biết $AB = BC = a$, $AD = 2a,\,$$SA = \dfrac{{3a\sqrt 2 }}{2}$, $SA \bot \left( {ABCD} \right)$. Gọi M, N theo thứ tự là trung điểm của SB, SA. Khoảng cách từ N đến mặt phẳng (MCD) bằng:
Trong không gian Oxyz, cho mặt cầu $\left( S \right):{\left( {x - 1} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z - 2} \right)^2} = 16$ và điểm $A\left( {1;2;3} \right)$. Ba mặt phẳng thay đổi đi qua A và đôi một vuông góc với nhau cắt mặt cầu theo ba đường tròn. Gọi S là tổng diện tích của ba hình tròn đó. Khi đó S bằng:
Cho hàm số $f\left( x \right) = m{x^3} - 3m{x^2} + \left( {3m - 2} \right)x + 2 - m$ với m là tham số thực. Có bao nhiêu giá trị nguyên của tham số m $ \in \left[ { - 10;10} \right]$ để hàm số $g\left( x \right) = \left| {f\left( x \right)} \right|$ có 5 điểm cực trị?
Tìm họ nguyên hàm của hàm số $f\left( x \right) = {x^2}{e^{{x^3} + 1}}$.
Phương trình ${7^{2{x^2} + 5x + 4}} = 49$ có tổng tất cả các nghiệm bằng
Đường cong như hình vẽ là đồ thị của hàm số nào?
Cho hình chóp đều $S.ABCD$ có cạnh $AB = a$, góc giữa đường thẳng $SA$ và mặt phẳng $\left( {ABC} \right)$ bằng $45^0$. Thể tích khối chóp $S.\,ABCD$ là
Họ nguyên hàm của hàm số $f\left( x \right) = \dfrac{1}{{5x + 4}}$ là
Trong không gian Oxyz, cho hai điểm $A\left( {1; - 1;2} \right),B\left( {3; - 4; - 2} \right)$ và đường thẳng $d:\left\{ \begin{array}{l}x = 2 + 4t\\y = - 6t\\z = - 1 - 8t\end{array} \right.$. Điểm $I\left( {a;b;c} \right)$ thuộc d là điểm thỏa mãn $IA + IB$ đạt giá trị nhỏ nhất. Khi đó $T = a + b + c$ bằng:
Cho hai số phức ${z_1}$ và ${z_2}$ thỏa mãn $\left| {{z_1}} \right| = 3,\,\left| {{z_2}} \right| = 4,\,\left| {{z_1} - {z_2}} \right| = \sqrt {41} $. Xét số phức $z = \dfrac{{{z_1}}}{{{z_2}}} = a + bi,\,\,\left( {a,b \in \mathbb{R}} \right)$. Khi đó $\left| b \right|$ bằng:
Cho hàm số $f\left( x \right)$ liên tục trên $\mathbb{R}$ có đạo hàm thỏa mãn $f'\left( x \right) + 2f\left( x \right) = 1,\,\,\forall x \in \mathbb{R}$ và $f\left( 0 \right) = 1$. Tích phân $\int\limits_0^1 {f\left( x \right)dx} $ bằng:

.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
