Đề thi thử THPT QG năm 2022 môn Toán online - Đề thi của Trường THPT Lương Văn Can
Vui lòng cài đặt đề thi trước khi làm bài
Họ các nguyên hàm $F(x)$ của hàm số $f(x) = 3\sin x + \dfrac{2}{x} - {e^x}$ là
Hàm số $y = {x^3} - 3x - 2019$ đồng biến trên khoảng
Cho cấp số cộng $\left( {{u_n}} \right)$ có số hạng đầu ${u_1} = 2$ và công sai $d = 5.$ Giá trị ${u_4}$ bằng
Cho hình nón đỉnh $S$ có bán kính đáy bằng $a\sqrt 2 .$ Mặt phẳng $\left( P \right)$ qua $S$ cắt đường tròn đáy tại $A,B$ sao cho $AB = 2a.$ Biết rằng khoảng cách từ tâm đường tròn đáy đến mặt phẳng $\left( P \right)$ là $\dfrac{{4a\sqrt {17} }}{{17}}.$ Thể tích khối nón bằng
Với $k$ và $n$ là hai số nguyên dương tùy ý thỏa mãn $k \le n$. Mệnh đề nào dưới đây đúng?
Cho hàm số $f(x)$ thỏa mãn $f\left( x \right) + 2\sqrt x f'\left( x \right) = 3x{e^{ - \sqrt x }},\forall x \in \left[ {0; + \infty } \right).$ Giá trị $f(1)$ bằng
Trong không gian$Oxyz,$ cho $\vec u = 3\vec i - 2\vec j + 2\vec k$. Tọa độ của $\vec u$ là
Họ nguyên hàm của hàm số $f\left( x \right) = {x^2}$ là
Tập nghiệm của bất phương trình ${\left( {0,1} \right)^{{x^2} + x}} > 0,01$ là
Cho hình chóp $S.ABCD$ có đáy là hình vuông cạnh $a$, $SA \bot (ABCD)$ và $SA = a\sqrt 6 .$ Giá trị $\cos (\widehat {SC,(SAD)})$ bằng
Cho số phức $z$ thỏa mãn $(2i - 1)z = 4 - 3i.$ Điểm biểu diễn của số phức $\overline z $ là
Nghiệm của phương trình ${2^x} = 16$ là
Giả sử $a,b$ là các số thực sao cho ${x^3} + {y^3} = a{.10^{3z}} + b{.10^{2z}}$ đúng với mọi các số thực dương $x,y,z$ thoả mãn $\log \left( {x + y} \right) = z$ và $\log \left( {{x^2} + {y^2}} \right) = z + 1.$ Giá trị của $a + b$ bằng
Cho hàm số $y = f(x)$ có đạo hàm $f'(x) = x{(x + 1)^2}{(x - 3)^3},\forall x \in \mathbb{R}$. Số điểm cực trị của hàm số là
Đạo hàm của hàm số $f\left( x \right) = {\log _2}\left( {3{x^2} + 2} \right)$ là
Hàm số $y = - {x^4} + 2{x^2} + 5$ đồng biến trên khoảng
Tập xác định của hàm số $y = {\left( {{3^x} - 9} \right)^{ - 2}}$ là
Cho $\int\limits_1^2 {f\left( x \right)} {\rm{d}}x = 2$ và $\int\limits_1^2 {\left[ {2f\left( x \right) - g\left( x \right)} \right]} {\rm{d}}x = 3;$ giá trị $\int\limits_1^2 {g\left( x \right)} {\rm{d}}x$ bằng
Lớp 12A có 35 học sinh, trong đó có 3 học sinh cùng tên là Trang, 2 học sinh cùng tên là Huy. Xếp ngẫu nhiên 35 học sinh thành một hàng dọXác suất để 3 học sinh tên Trang đứng cạnh nhau và 2 học sinh tên Huy đứng cạnh nhau là
Gọi ${z_1}$ và ${z_2}$ là hai nghiệm phức của phương trình ${z^2} + 2z + 10 = 0$. Giá trị biểu thức $\left| {{z_1}} \right| + \left| {{z_2}} \right|$ bằng
Kí hiệu ${z_1},{z_2}$ là hai nghiệm phức của phương trình ${{\rm{z}}^2} + z + {2019^{2018}} = 0.$ Giá trị $\left| {{z_1}} \right| + \left| {{z_2}} \right|$ bằng
Số giao điểm của đồ thị hàm số $y = {x^3} - 3x + 1$ và đường thẳng $y = 3$ là
Cho lăng trụ tam giác đều $ABC.A'B'C'$ có cạnh đáy bằng $2a,$ $O$ là trọng tâm tam giác $ABC$ và $A'O = \dfrac{{2a\sqrt 6 }}{3}.$ Thể tích của khối lăng trụ $ABC.A'B'C'$ bằng
Cho hàm số $y = f\left( x \right)$ liên tục trên ${\rm{[}}1;2{\rm{]}}.$ Quay hình phẳng $\left( H \right) = \left\{ {y = f(x),y = 0,x = 1,x = 2} \right\}$ xung quanh trục $Ox$ được khối tròn xoay có thể tích
Cho hai điểm $A( - 1;0;1),B( - 2;1;1).$ Phương trình mặt phẳng trung trực của đoạn $AB$ là
Đường thẳng $d:\left\{ \begin{array}{l}x = 1 - 2t\\y = 2 + 3t\\z = 3\end{array} \right.$,$\left( {t \in \mathbb{R}} \right)$ có một vectơ chỉ phương là
Tích các nghiệm thực của phương trình $\log _2^2x + \sqrt {3 - {{\log }_2}x} = 3$ bằng
:
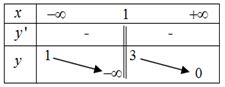
Cho hàm số $y = f(x)$ có bảng biến thiên như hình bên. Số nghiệm của phương trình $3f(x) - 2 = 0$ là
Cho $\int\limits_{ - 1}^4 {x\ln \left( {x + 2} \right){\rm{d}}x} = a\ln 6 + \dfrac{5}{b}$ với $a,b$ là các số nguyên dương. Giá trị $2a + 3b$ bằng
Cho ba điểm $A( - 2;0;0),\;B\left( {0;1;0} \right),\;C\left( {0;0; - 3} \right).$ Đường thẳng đi qua trực tâm $H$ của tam giác $ABC$ và vuông góc với ${\rm{mp}}\left( {ABC} \right)$ có phương trình là
Cho hình chóp tứ giác đều $S.ABCD$ cạnh đáy bằng $a.$ Gọi $E$ là điểm đối xứng với $D$ qua trung điểm của ${\rm{S}}A;$$M,N$lần lượt là trung điểm $AE,BC.$ Khoảng cách giữa hai đường thẳng $MN,\;SC$ bằng
Cho đường thẳng $d:\dfrac{x}{6} = \dfrac{{y - 1}}{3} = \dfrac{z}{2}$ và ba điểm $A(2;0;0),\;B(0;4;0),\;C(0;0;6).$ Điểm $M(a;b;c) \in d$ thỏa mãn $MA + 2MB + 3MC$ đạt giá trị nhỏ nhất. Tính $S = a + b + c.$
Trong các mặt cầu tiếp xúc với hai đường thẳng ${\Delta _1}:\left\{ \begin{array}{l}x = t\\y = 2 - t\\z = - 4 + 2t\end{array} \right.,\;{\Delta _2}:\left\{ \begin{array}{l}x = - 8 + 2t\\y = 6 + t\\z = 10 - t\end{array} \right.;$ phương trình mặt cầu có bán kính nhỏ nhất là
Cho hàm số $y = \left| {{x^3} - m{x^2} + 9} \right|$. Gọi $S$ là tập tất cả các số tự nhiên $m$ sao cho hàm số đồng biến trên $\left[ {2; + \infty } \right)$. Tổng các phần tử của $S$ là
Cho hàm số $y = f(x)$ có đạo hàm liên tục trên $\mathbb{R},$ hàm số $y = f'(x)$ có đồ thị như hình vẽ. Số điểm cực trị của hàm số $y = f(1 - x)$ là
Cho hàm số $y = f(x)$ có bảng biến thiên trên đoạn $\left[ { - 1;5} \right]$ như hình vẽ. Có bao nhiêu giá trị nguyên của $m$ để phương trình $f\left( {3\sin x + 2} \right) = m$ có đúng 3 nghiệm phân biệt trên khoảng $\left( { - \dfrac{\pi }{2};\pi } \right)$?
Cho hai điểm $A(3; - 1;2)$ và $B(5;3; - 2).$ Mặt cầu nhận đoạn $AB$ làm đường kính có phương trình là
Cho đường thẳng $d:\dfrac{{x - 1}}{1} = \dfrac{{y - 1}}{2} = \dfrac{{z - 1}}{2}$ và hai điểm $A\left( {2;0; - 3} \right),B\left( {2; - 3;1} \right).$ Đường thẳng $\Delta $ qua $A$ và cắt $d$ sao cho khoảng cách từ $B$ đến $\Delta $ nhỏ nhất. Phương trình của $\Delta $ là
Cho số phức $z$ thỏa mãn $\left| {z + \sqrt {15} } \right| + \left| {z - \sqrt {15} } \right| = 8$ và $\left| {z + \sqrt {15} i} \right| + \left| {z - \sqrt {15} i} \right| = 8.$ Tính $\left| z \right|.$
Cho lăng trụ $ABC.A'B'C'$ có đáy $ABC$ là tam giác vuông đỉnh $A$,$AB = AC = a.$ Hình chiếu vuông góc của $A'$ lên mặt phẳng $\left( {ABC} \right)$ là điểm $H$ thuộc đoạn $BC.$ Khoảng cách từ $A$ đến mặt phẳng $\left( {BCC'B'} \right)$ bằng $\dfrac{{a\sqrt 3 }}{3}.$ Thể tích khối lăng trụ $ABC.A'B'C'$ bằng
Cho ${\log _2}b = 4,\,\;{\log _2}c = - 4;$ khi đó ${\log _2}({b^2}c)$ bằng
Mặt phẳng $\left( P \right):2x - y + 3z - 1 = 0$ có một vectơ pháp tuyến là
Cho hàm số $y = f\left( x \right)$ liên tục trên $\mathbb{R}$ và có đồ thị như hình bên. Tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số $g\left( x \right) = f\left( {2\sin \,\dfrac{x}{2}\cos \dfrac{x}{2} + 3} \right)$ bằng
:
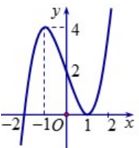
Cho hàm số $y = f\left( x \right)$ có đồ thị $\left( C \right)$ như hình vẽ. Số giao điểm của $\left( C \right)$ và đường thẳng $y = 3$ là:
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau: Mệnh đề nào dưới đây sai?
Họ nguyên hàm của hàm số $f\left( x \right) = \dfrac{1}{x} + \dfrac{1}{{{x^3}}}$ là:
Trong không gian Oxyz, cho điểm $M\left( {2017;2018;2019} \right)$. Hình chiếu vuông góc của điểm M trên trục Oz có tọa độ là:
Thể tích khối tròn xoay được tạo thành khi quay quanh trục Ox hình phẳng (H) được giới hạn bởi các đường $y = f\left( x \right)$ liên tục trên đoạn $\left[ {a;b} \right]$, trục Ox và hai đường thẳng $x = a,x = b$ là:
Cho hàm số $y = {\log _a}x,\,\,\,0 < a \ne 1$. Khẳng định nào sau đây đúng?

.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
