Đề thi thử THPT QG năm 2022 môn Toán online - Đề thi của Trường THPT Lê Quảng Chí
Vui lòng cài đặt đề thi trước khi làm bài
Tìm hệ số của số hạng không chứa x trong khai triển ${\left( {\frac{x}{2} + \frac{4}{x}} \right)^{18}}$ với $x \ne 0$
Cho hình lăng trụ tam giác đều $ABC.A'B'C'$ có $AB = 2a,\,\,AA' = a\sqrt 3 $ Tính thể tích $V$ của khối lăng trụ $ABC.A'B'C'$ theo $a$ ?
Tìm số giá trị nguyên thuộc đoạn $\left[ { - 2019;2019} \right]$ của tham số $m$ để đồ thị hàm số $y = \dfrac{{\sqrt {x - 3} }}{{{x^2} + x - m}}$ có đúng hai đường tiệm cận.
Cho đa thức $f\left( x \right) = {\left( {1 + 3x} \right)^n} = {a_0} + {a_1}x + {a_2}{x^2} + ... + {a_n}{x^n}\left( {n \in {{\rm N}^*}} \right).$ Tìm hệ số ${a_3}$ biết rằng ${a_1} + 2{a_2} + ... + n{a_n} = 49152n.$
Tìm tất cả các giá trị của tham số $m$ để phương trình$\frac{1}{3}\left| {co{s^3}x} \right| - 3co{s^2}x + 5\left| {\cos x} \right| - 3 + 2m = 0$có đúng bốn nghiệm phân biệt thuộc đoạn $\left[ {0;2\pi } \right]$
:
Cho hàm số $y = \frac{{ax + b}}{{cx + d}}\left( {a \ne 0} \right)$ có đồ thị như hình vẽ bên dưới.
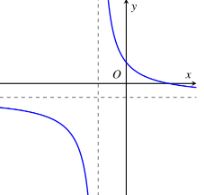
Cho hình chóp tứ giác đều $S.ABCD$ có cạnh đáy bằng $a$ và chiều cao bằng $a\sqrt 2 $. Tính khoảng cách từ tâm $O$ của đáy $ABCD$ đến một mặt bên theo $a.$
Cho tích phân $I = \int\limits_0^4 {f\left( x \right)dx = 32.} $ Tính tích phân $J = \int\limits_0^2 {f\left( {2x} \right)} dx$
Tính tổng $T$ của các giá trị nguyên của tham số $m$ để phương trình ${e^x} + \left( {{m^2} - m} \right){e^{ - x}} = 2m$ có đúng hai nghiệm phân biệt nhỏ hơn $\frac{1}{{\log e}}.$
Cho hàm số $f\left( x \right) = \left\{ \begin{array}{l}\frac{{\sqrt {{x^2} + 4} - 2}}{{{x^2}}}\,\,\,khi\,x \ne 0\\2a - \frac{5}{4}\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,x = 0\end{array} \right.$ . Tìm giá trị thực của tham số $a$ để hàm số $f\left( x \right)$ liên tục tại $x = 0$.
Cho mặt cầu tâm $O$ và tam giác $ABC$ có ba đỉnh nằm trên mặt cầu với góc $\angle BAC = {30^0}$ và $BC = a$ . Gọi $S$ là điểm nằm trên mặt cầu, không thuộc mặt phẳng $\left( {ABC} \right)$ và thỏa mãn $SA = SB = SC,$ góc giữa đường thẳng $SA$ và mặt phẳng $\left( {ABC} \right)$ bằng ${60^0}$ . Tính thể tích $V$ của khối cầu tâm $O$ theo $a.$
Cho tích phân $I = \int\limits_0^2 {f\left( x \right)dx = 2} .$ Tính tích phân $J = \int\limits_0^2 {\left[ {3f\left( x \right) - 2} \right]} dx$ .
Gọi $F\left( x \right)$ là nguyên hàm trên $\mathbb{R}$ của hàm số $f\left( x \right) = {x^2}{e^{a\,x}}\left( {a \ne 0} \right),$ sao cho $F\left( {\frac{1}{a}} \right) = F\left( 0 \right) + 1$. Chọn mệnh đề đúng trong các mệnh đề sau.
Tìm giá trị thực của tham số $m$ để hàm số $y = {x^3} - 3{x^2} + mx$ đạt cực đại tại $x = 0$
Trong các hàm số dưới đây, hàm số nào nghịch biến trên tập số thực $\mathbb{R}$ ?
Gọi $l,h,\,r$ lần lượt là độ dài đường sinh, chiều cao và bán kính mặt đáy của một hình nón. Tính diện tích xung quanh ${S_{xq}}$ của hình nón đó theo $l,h,\,r$.
Tìm tập nghiệm $S$ của bất phương trình ${\left( {\frac{1}{2}} \right)^{ - {x^2} + 3x}} < \frac{1}{4}$
Cho hình lăng trụ $ABC.A'B'C'$ có đáy là tam giác đều cạnh $a,\,AA' = \frac{{3a}}{2}.$ Biết rằng hình chiếu vuông góc của điểm $A'$ lên mặt phẳng $\left( {ABC} \right)$ là trung điểm của cạnh $BC.$ Tính thể tích $V$ của khối lăng trụ đó theo $a.$
Tính diện tích $S$ của hình phẳng $\left( H \right)$ giới hạn bởi các đường cong $y = - {x^3} + 12x$ và $y = - {x^2}$
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như bên dưới. Mệnh đề nào dưới đây Sai?
Cho hàm số $F\left( x \right)$ là một nguyên hàm của hàm số $f\left( x \right) = \frac{{2\cos x - 1}}{{{{\sin }^2}x}}$ trên khoảng $\left( {0;\pi } \right).$ Biết rằng giá trị lớn nhất của $F\left( x \right)$ trên khoảng $\left( {0;\pi } \right)$ là $\sqrt 3 $. Chọn mệnh đề đúng trong các mệnh đề sau?
Cho hàm số $f\left( x \right)$ có đạo hàm trên $\mathbb{R}$ là $f'\left( x \right) = \left( {x - 1} \right)\left( {x + 3} \right).$ Có bao nhiêu giá trị nguyên của tham số $m$ thuộc đoạn $\left[ { - 10;20} \right]$ để hàm số $y = f\left( {{x^2} + 3x - m} \right)$ đồng biến trên khoảng $\left( {0;2} \right)?$
Cho hình lập phương $ABCD.A'B'C'D'.$ Biết tích của khoảng cách từ điểm $B'$ và điểm $D$ đến mặt phẳng $\left( {D'AC} \right)$ bằng $6{a^2}\left( {a > 0} \right)$ . Giả sử thể tích của khối lập phương $ABCD.A'B'C'D'$ là $k{a^3}.$ Chọn mệnh đề đúng trong các mệnh đề sau.
Cho cấp số cộng $\left( {{u_n}} \right)$ với số hạng đầu ${u_1} = - 6$ và công sai $d = 4$. Tính tổng $S$ của 14 số hạng đầu tiên của cấp số cộng đó.
Một khối trụ có thể tích bằng $25\pi .$ Nếu chiều cao hình trụ tăng lên năm lần và giữa nguyên bán kính đáy thì được một hình trụ mới có diện tích xung quanh bằng $25\pi $ . Tính bán kính đát $r$ của hình trụ ban đầu.
Tìm số hạng đầu ${u_1}$ của cấp số nhân $\left( {{u_n}} \right)$ biết rằng ${u_1} + {u_2} + {u_3} = 168$ và ${u_4} + {u_5} + {u_6} = 21.$
Cho hàm số $y = \frac{{mx + 1}}{{x - 2m}}$ với tham số $m \ne 0$. Giao điểm của hai đường tiệm cận của đồ thị hàm số thuộc đường thẳng có phương trình nào dưới đây?
Trong không gian cho tam giác $OIM$ vuông tại $I,$ góc $\angle IOM = {45^0}$ và cạnh $IM = a.$ Khi quay tam giác $OIM$ quanh cạnh góc vuông $OI$ thì đường gấp khúc $OMI$ tạo thành một hình nón tròn xoay. Tính diện tích xung quanh ${S_{xq}}$ của hình nón tròn xoay đó theo $a.$
Cho khối nón có bán kính đáy $r = 3,$ chiều cao $h = \sqrt 2 .$ Tính thể tích $V$ của khối nón.
Cho tập hợp $S = \left\{ {1;2;3;4;5;6} \right\}.$ Gọi $M$ là tập hợp các số tự nhiên có 6 chữ số đôi một khác nhau lấy từ $S$ sao cho tổng chữ số các hàng đơn vị, hàng chục và hàng trăm lớn hơn tổng chữ số các hàng còn lại là 3. Tính tổng $T$ của các phần tử của tập hợp $M.$
Cho tích phân $\int_1^2 {\frac{{\ln x}}{{{x^2}}}dx = \frac{b}{c} + a\ln 2} $ với $a$ là số thực, $b$ và $c$ là các số nguyên dương, đồng thời $\frac{b}{c}$ là phân số tối giản. Tính giá trị của biểu thức $P = 2a + 3b + c$
Cho hàm số $y = \frac{1}{3}{x^3} - 2m{x^2} + \left( {m - 1} \right)x + 2{m^2} + 1$ $(m$ là tham số). Xác định khoảng cách lớn nhất từ gốc tọa độ $O\left( {0;0} \right)$ đến đường thẳng đi qua hai điểm cực trị của đồ thị hàm số trên.
Gieo đồng thời hai con súc sắc cân đối và đồng chất. Tính xác suất $P$ để hiệu số chấm trên các mặt xuất hiện của hai con súc sắc bằng 2.
Cho hình chóp $S.ABCD$ có đường thẳng $SA$ vuông góc với mặt phẳng $\left( {ABCD} \right)$ , đáy $ABCD$ là hình thang vuông tại $A$ và $B$ , có $AB = a,\,AD = 2a,BC = a.$ Biết rằng $SA = a\sqrt 2 .$ Tính thể tích $V$ của khối chóp $S.BCD$ theo $a.$
Cho chiếc trống như hình vẽ, có đường sinh là nửa elip được cắt bởi trục lớn với độ dài trục lơn bằng $80cm,$ độ dài trục bé bằng $60cm$ . Tính thể tích $V$ của trống (kết quả làm tròn đến hàng đơn vị)
Cho lăng trụ đứng tam giác $ABC.A'B'C'$ . Gọi $M,{\rm N},P,Q$ là các điểm lần lượt thuộc các cạnh $AA',\,BB',CC',\,B'C'$ thỏa mãn $\frac{{AM}}{{AA'}} = \frac{1}{2},\,\frac{{B{\rm N}}}{{BB'}} = \frac{1}{3},\,\frac{{CP}}{{CC'}} = \frac{1}{4},\,\,\frac{{C'Q}}{{C'B'}} = \frac{1}{5}$. Gọi ${V_1},\,{V_2}$ lần lượt là thể tích khối tứ diện $MNPQ$ và khối lăng trụ $ABC.A'B'C'.$ Tính tỷ số $\frac{{{V_1}}}{{{V_2}}}.$
Trong mặt phẳng với hệ trục tọa độ $Oxy,$ cho đường thẳng $d$ cắt hai trục $Ox$ và $Oy$ lần lượt tại 2 điểm $A\left( {a;0} \right)$ và $B\left( {0;b} \right)$ $\left( {a \ne 0,\,\,b \ne 0} \right)$. Viết phương trình đường thẳng $d$.
Gọi $m$ và $M$ lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số $y = x - \sqrt {4 - {x^2}} $. Tính tổng $M + m$.
Tính giới hạn $L = \lim \dfrac{{{n^3} - 2n}}{{3{n^2} + n - 2}}$.
Gọi $T$ là tổng các nghiệm của phương trình $\log _{\frac{1}{3}}^2x - 5{\log _3}x + 4 = 0$. Tính $T$ .
Tìm nghiệm của phương trình ${\sin ^4}x - {\cos ^4}x = 0$.
Tìm điều kiện cần và đủ của $a,\,\,b,\,\,c$ để phương trình $a\sin x + b\cos x = c$ có nghiệm?
Tìm tập xác định $D$ của hàm số$y = {\left( {{x^2} - 1} \right)^{ - 4}}$.
Hình vẽ bên là đồ thị của hàm số nào trong các hàm số dưới đây?
Cho $a > 0$, $b > 0$ thỏa mãn ${a^2} + 4{b^2} = 5ab$. Khẳng định nào sau đây đúng?
Cho tập $A$ có $26$ phần tử. Hỏi $A$ có bao nhiêu tập con gồm $6$ phần tử?
:
Cho hàm số $y = f\left( x \right)$ liên tục trên $\mathbb{R}$ và có đồ thị như hình vẽ. Mệnh đề nào sau đây SAI?
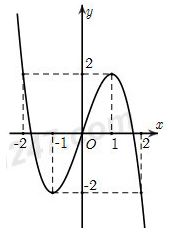
Cho hàm số $f\left( x \right) = 2x + {e^x}$. Tìm một nguyên hàm $F\left( x \right)$ của hàm số $f\left( x \right)$ thỏa mãn $F\left( 0 \right) = 2019$.
Tập tất cả giá trị của tham số $m$ để hàm số $y = {x^3} - 3m{x^2} + 3x + 1$ đồng biến trên $\mathbb{R}$ là
Cho $a$, $b$ là các số dương thỏa mãn ${\log _9}a = {\log _{16}}b = {\log _{12}}\dfrac{{5b - a}}{2}$. Tính giá trị $\dfrac{a}{b}$.

.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
