Đề thi thử học kỳ 2 môn Toán lớp 12 online - Mã đề 02
Vui lòng cài đặt đề thi trước khi làm bài
Trong không gian $Oxyz$, các vectơ đơn vị trên các trục $Ox$, $Oy$, $Oz$ lần lượt là $\vec{i}$, $\vec{j}$, $\vec{k}$, cho điểm $M\left( 3;-4;12 \right)$? Mệnh đề nào sau đây đúng?
Trong không gian $Oxyz$, đường thẳng đi qua điểm $A\left( 3;1;2 \right)$ và vuông góc với mặt phẳng $x+y+3z+5=0$ có phương trình là
Trong không gian $Oxyz$, một vectơ pháp tuyến của mặt phẳng $\frac{x}{-5}+\frac{y}{1}+\frac{z}{-2}=1$ là
Họ nguyên hàm của hàm số $f\left( x \right)=3{{x}^{2}}-2x+3$ là
$\int{{{\text{e}}^{-2x+1}}}\text{d}x$ bằng
Cho hình phẳng $\left( H \right)$ được giới hạn bởi các đường $x=0$, $x=\pi $, $y=0$ và $y=-\cos x$. Tính thể tích $V$ của khối tròn xoay tạo thành khi quay $\left( H \right)$ xung quanh trục $Ox$ được tính theo công thức:
Trong không gian $Oxyz$, viết phương trình đường thẳng đi qua điểm $A\left( 1;2;3 \right)$ và có vectơ chỉ phương $\vec{u}=\left( 2;-1;-2 \right)$.
Nghiệm phức có phần ảo dương của phương trình ${{z}^{2}}-2z+5=0$ là:
Cho các số phức ${{z}_{1}}=3+4i$, ${{z}_{2}}=5-2i$. Tìm số phức liên hợp $\bar{z}$ của số phức $z=2{{z}_{1}}+3{{z}_{2}}$
Phần thực của số phức $\left( 2-i \right)\left( 1+2i \right)$ là:
Trong không gian với hệ tọa độ $Oxyz$, cho mặt cầu $\left( S \right)$ có tâm $I\left( 1;2;1 \right)$ và cắt mặt phẳng $\left( P \right):2x-y+2z+7=0$ theo một đường tròn có đường kính bằng $8$. Phương trình mặt cầu là
Số phức liên hợp $\bar{z}$ của số phức $z=\frac{4+6i}{1-i}$ là
Tìm nguyên hàm $F\left( x \right)$ của $f\left( x \right)={{\tan }^{2}}x$ biết phương trình $F\left( x \right)=0$ có một nghiệm $\frac{\pi }{4}$.
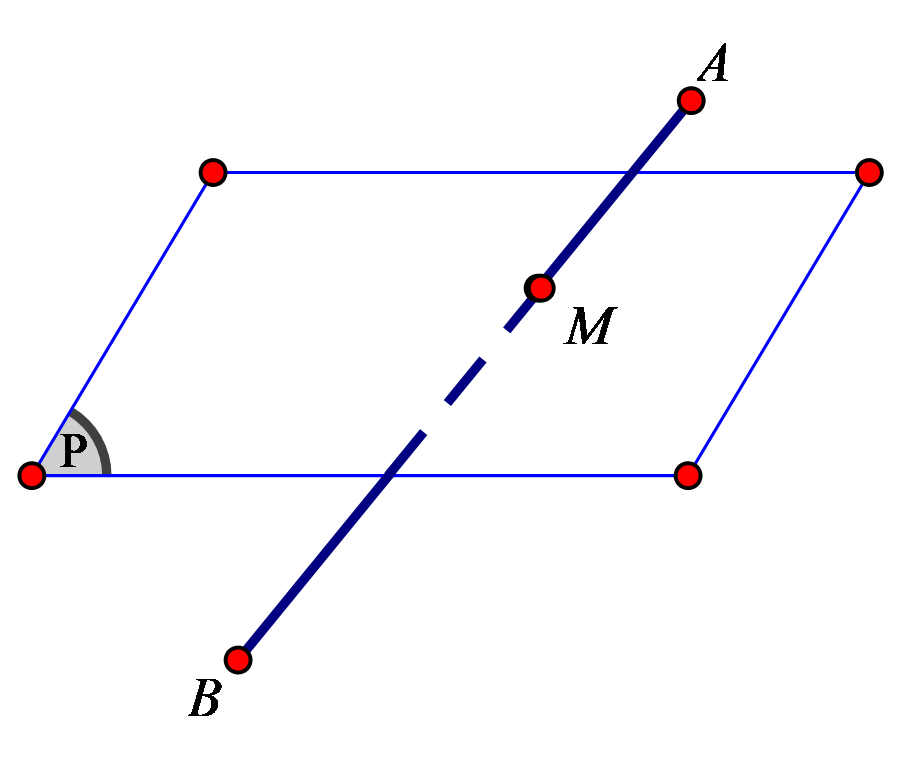
Trong không gian $Oxyz,$ cho hai đường thẳng $\frac{x-2}{1}=\frac{y-4}{1}=\frac{z}{-2}$ và $\frac{x-3}{2}=\frac{y+1}{-1}=\frac{z+2}{-1}$ .Gọi là trung điểm của đoạn vuông góc chung của hai đường thẳng trên. Tính độ dài đoạn thẳng $OM.$
Gọi $S$ là diện tích hình phẳng giới hạn bởi các đường $y=-{{3}^{x}},y=0$, $x=0,x=4$. Mệnh đề nào sau đây đúng
Cho hai số phức ${{z}_{1}}=-1+2i$, ${{z}_{2}}=1+2i$. Tính $T={{\left| {{z}_{1}} \right|}^{2}}+{{\left| {{z}_{2}} \right|}^{2}}$
Trong không gian $Oxyz$, cho mặt phẳng $\left( P \right)$ có phương trình $2x-6y-4z+7=0$ và ba điểm $A\left( 2;4;-1 \right),B\left( 1;4;-1 \right),C\left( 2;4;3 \right)$. Gọi $S$ là điểm thuộc mặt phẳng $\left( P \right)$ sao cho $SA=SB=SC$. Tính $l=SA+SB$
Trong không gian $Oxyz$, tọa độ tâm $I$ và bán kính $R$ của mặt cầu $\left( S \right):{{x}^{2}}+{{y}^{2}}+{{z}^{2}}-4x+2y+2z-3=0$ là
Diện tích của hình phẳng giới hạn bởi đồ thị hàm số $y={{x}^{2}}-4$ và các đường thẳng $y=0$, $x=-1$, $x=5$ bằng
Trong không gian $Oxyz$, cho ba điểm $A\left( 0;0;1 \right)$, $B\left( 0;2;0 \right)$, $C\left( 3;0;0 \right)$. Gọi $H\left( x;y;z \right)$ là trực tâm của tam giác $ABC$. Giá trị của $x+2y+z$ bằng
Trong không gian $Oxyz$, cho mặt phẳng $\left( P \right)$: $3x+4y-12z+5=0$ và điểm $A\left( 2;4;-1 \right)$. Trên mặt phẳng $\left( P \right)$ lấy điểm $M$. Gọi $B$ là điểm sao cho $\overrightarrow{AB}=3\overrightarrow{AM}$. Tính khoảng cách $d$ từ $B$ đến mặt phẳng $\left( P \right)$.
Trong không gian $Oxyz$, cho bốn điểm $A\left( 0;1;-1 \right)$, $B\left( 1;1;2 \right)$, $C\left( 1;-1;0 \right)$ và $D\left( 0;0;1 \right)$. Mặt phẳng $\left( \alpha \right)$ song song với mặt phẳng $\left( BCD \right)$ và chia khối tứ diện $ABCD$ thành hai khối đa diện sao cho tỉ số thể tích của khối đa diện có chứa điểm $A$ và khối tứ diện $ABCD$ bằng $\frac{1}{27}$. Viết phương trình mặt phẳng $\left( \alpha \right)$.
Trong không gian $Oxyz$ biết vector $\overrightarrow{n}=\left( a;b;c \right)$ là vector pháp tuyến của mặt phẳng đi qua điểm $A\left( 2;1;5 \right)$ và chứa trục $Ox$ . Khi đó tính $k=\frac{b}{c}$ .
$A,\,B$ là hai điểm biểu diễn của hai nghiệm đó trên mặt phẳng $Oxy$ . Biết tam giác $OAB$ đều (với $O$ là gốc tọa độ), tính $P=c+2d$ .
Cho ${{z}_{1}}$và ${{z}_{2}}$ là hai nghiệm phức của phương trình ${{z}^{2}}-2z+5=0$, biết ${{z}_{1}}-{{z}_{2}}$ có phần ảo là số thực âm. Tìm phần ảo của số phức $\text{w}=2z_{1}^{2}-z_{2}^{2}$ .
Biết $\int\limits_{0}^{\frac{\pi }{4}}{\left( {{\tan }^{2}}x+2{{\tan }^{8}}x \right)}dx=\frac{-a}{b}+\frac{\pi }{c}$ với $a,b,c\in \mathbb{N}$, phân số $\frac{a}{b}$ tối giản. Tính $T=a+b+c$.
Trong không gian $\text{Ox}yz$, tính diện tích $S$ của tam giác $ABC$, biết $A\left( 2;0;0 \right),\ B\left( 0;3;0 \right)$, $C\left( 0;0;4 \right)$.
Gọi $z$ là số phức có mô đun nhỏ nhất thỏa mãn điều kiện $\left| z-2-8i \right|=\sqrt{17}$. Biết $z=a+bi$
với $a,b\in \mathbb{R}$, tính $m=2{{a}^{2}}-3b$.
Trên tập số phức, phương trình ${{z}^{2}}-6z+{{2019}^{2020}}+9=0$ có một nghiệm là
Tính môđun $\left| z \right|$ của số phức$z=\left( 2+i \right){{\left( 1+i \right)}^{2}}+1$

.png)
