Trang chủ
lop-12
toan
Đề thi thử giữa học kỳ 1 môn Toán lớp 12 online - Mã đề 11

Đề thi thử giữa học kỳ 1 môn Toán lớp 12 online - Mã đề 11

Cài đặt đề thi

Thời gian làm bài

Không tính giờ

Tính giờ

phút

Chưa xem
Đã trả lời

Bạn có thể thử làm lại bài thi lần nữa

Trả lời đúng
Trả lời sai

Câu đúng

Câu sai

Điểm của bạn là

Làm lại lần nữa

Làm đề khác

Danh sách câu hỏi

Bấm vào ô số để xem câu hỏi

Vui lòng cài đặt đề thi trước khi làm bài

Câu 1

Hỏi hàm số $y=2 x^{4}-5$ đồng biến trên khoảng nào?

A. $(0 ;+\infty)$

B. $\left(-\infty ;-\frac{1}{2}\right)$

C. $(-\infty ; 0)$

D. $\left(-\frac{1}{2} ;+\infty\right)$

Lời giải :

Ta có $y^{\prime}=8 x^{3}, y^{\prime}>0 \Leftrightarrow x>0$

Nên hàm số đã cho đồng biến trên $(0 ;+\infty)$

Câu 2

Số điểm cực trị của hàm số $y=-x^{3}+3 x^{2}+x+3$ là

A. 2

B. 3

C. 1

D. 0

Lời giải :

$y^{\prime}=-3 x^{2} +6 x+1$ có hai nghiệm phân biệt nên hàm số có hai điểm cực trị.

Câu 3

Tìm giá trị lớn nhất của hàm số $y=-x^{3}+3 x^{2}$ trên đoạn [-3;1]

A. $\max\limits _{[-3 ; 1]} y=2$

B. $\max\limits _{[-3 ; 1]} y=0$

C. $\max \limits _{[-3 ; 1]} y=54$

D. $\max\limits _{[-3 ; 1]} y=54$

Lời giải :

$\begin{aligned} &y^{\prime}=-3 x^{2}+6 x=0 \Leftrightarrow x=0 \text { (thỏa mãn) hoặc } x=2 \text { (loại) }\\ &y(-3)=54 ; y(0)=0 ; y(1)=2\\ &\text {Vậy: } \max\limits _{[-3 ; 1]} y=54\end{aligned}$

Câu 4

Đồ thị hàm số $y=\frac{2 x+3}{x+2}$ có các đường tiệm cận là:

A. $y=-2\text{ và }x=-2 .$

B. $y=2\text{ và }x=-2$

C. $y=-2\text{ và }x=2$

D. $y=2\text{ và }x=2$

Lời giải :

Nhắc lại đồ thị hàm số $y=\frac{a x+b}{c x+d}$ có đường tiệm cận ngang là $y=\frac{a}{c}$ và đường tiệm cận đứng là $x=\frac{-d}{c}$ .

Vậy đồ thị hàm số có tiệm cận đứng là x=-2 và tiệm cận ngang y=2

Câu 5

Cho đồ thị như hình vẽ bên. Đây là đồ thị của hàm số nào?

A. $y=x^{3}+3 x^{2}$

B. $y=-x^{3}+3 x^{2}+1$

C. $y=-x^{3}+2x^{2}$

D. $y=x^{3}-3 x^{2}-2$

Lời giải :

Khi x tiến tới $+\infty$ thì y tiến tới $+\infty$ , do đó hệ số của x³ phải dương nên loại B, C

Đồ thị hàm số đi qua điểm (0;0) nên hàm số ở ý D không thỏa mãn

Câu 6

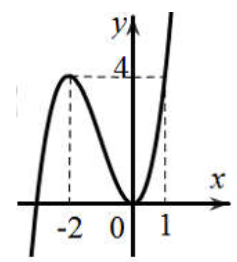
Khi tăng độ dài tất cả các cạnh của một khối hộp chữ nhật lên gấp ba thì thể tích khối hộp tương ứng sẽ:

A. tăng 3 lần.

B. Tăng 6 lần.

C. Tăng 9 lần.

D. Tăng 27 lần.

Lời giải :

Giả sử chiều dài, chiều rộng, chiều cao của khối hộp chữ nhật là a, b, c .

Thể tích của khối hộp là V =abc .

Khi tăng tất cả các cạnh của khối hộp lên gấp đôi thì thể tích khối hộp thu được là

$V^{\prime}=3 a \cdot 3 b \cdot 3 c=27 a b c=27 V$

Câu 7

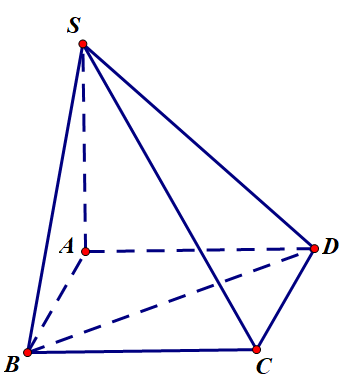
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A , $A B=3 a, A C=4 a$ , SB vuông góc (ABC), $S C= a\sqrt{41} $ . Tính thể tích khối chóp S.ABC theo a

A. $8 a^{3}$

B. $30 a^{3}$

C. $10 a^{3} \sqrt{2}$

D. $5 a^{3}$

Lời giải :

Ta có $S_{\Delta B C}=\frac{1}{2} \cdot A B \cdot A C=6a^2$

$BC = \sqrt {A{B^2} + A{C^2}} = 5a$

$S B=\sqrt{S C^{2}-B C^{2}}=4a$

Vậy $V_{S . A B C}=\frac{1}{3} \cdot S_{\triangle A B C} \cdot S B=8 a^{3}(\mathrm{dvtt})$

Câu 8

Cho hàm số y=f(x) có bảng biến thiên như hình vẽ bên. Khẳng định nào sau đây là đúng?

A. Hàm số f(x) đồng biến trên các khoảng $\begin{array}{l}(-\infty ; 1) \cup(1 ;+\infty)\end{array}$

B. Hàm số f(x) đồng biến trên $\mathbb{R}$

C. Hàm số f(x) đồng biến trên các khoảng $(-\infty ; 1) \text { và }(1 ;+\infty)$

D. Hàm số f(x) đồng biến trên các khoảng $(-\infty ; 2) \text { và }(2 ;+\infty)$

Lời giải :

Dựa vào bảng biến thiên ta có hàm số f(x) đồng biến trên các khoảng $(-\infty ; 1) \text { và }(1 ;+\infty)$

Câu 9

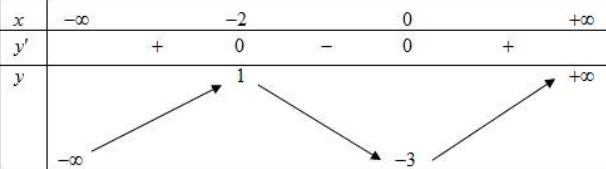
Cho hàm số y =f(x) có bảng biến thiên như sau:

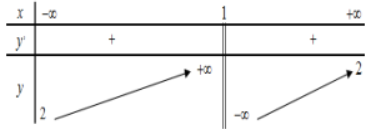
Hàm số y=f(x) nghịch biến trên khoảng nào dưới đây?

A. $(-2 ; 0)$

B. $(0 ;+\infty)$

C. $(-\infty ;-2)$

D. $(-3 ; 1)$

Lời giải :

Dựa vào bản biến thiên, trên khoảng (-2;0) thì y'<0 nên hàm số nghịch biến trên khoảng (-2;0)

Câu 10

Cho hàm số$y=f(x)$. Hàm số $y=f'(x)$ có đồ thị như hình vẽ

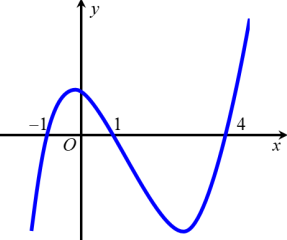
Hàm số $y=f\left(2-e^{x}\right)$ đồng biến trên khoảng:

A. $(0 ; \ln 3)$

B. $(2 ;+\infty)$

C. $(-\infty ; 1)$

D. $(1 ; 4)$

Lời giải :

$\begin{array}{l} \text { Ta có: } y=f\left(2-e^{x}\right) \Rightarrow y^{\prime}=-e^{x} f^{\prime}\left(2-e^{x}\right) \text { . } \\ f^{\prime}(x)=0 \Rightarrow\left[\begin{array}{l} 2-e^{x}=-1 \\ 2-e^{x}=1 \\ 2-e^{x}=4 \end{array} \Rightarrow\left[\begin{array}{l} x=\ln 3 \\ x=0 \\ e^{x}=-2(1) \end{array}\right.\right. \end{array}$

Bảng xét dấu đạo hàm:

Vậy hàm số đồng biến trên các khoảng $(-\infty ; 0) ;(\ln 3 ;+\infty)$

B thỏa

Câu 11

Cho hàm số $y=x^{3}+17 x^{2}-24 x+8$. Kết luận nào sau đây là đúng?

A. $x_{C D}=1$

B. $x_{C D}=\frac{2}{3}$

C. $x_{C D}=-3$

D. $x_{C D}=-12$

Lời giải :

$y^{\prime}=3 x^{2}+34 x-24=0 \Leftrightarrow\left[\begin{array}{l}x=-12 \\x=\frac{2}{3}\end{array}\right.$

Lập bảng biến thiên ta thấy hàm số đạt cực đại tại x = −12 .

Câu 12

Trong các hàm số sau, hàm số nào chỉ có cực đại mà không có cực tiểu?

A. $y=-10 x^{4}-5 x^{2}+7$

B. $y=-17 x^{3}+2 x^{2}+x+5$

C. $y=\frac{x-2}{x+1}$

D. $y=\frac{x^{2}+x+1}{x-1}$

Lời giải :

Hàm số $y=-10 x^{4}-5 x^{2}+7 \text { có } y^{\prime}=-40 x^{3}-10 x=0 \Leftrightarrow x=0 \text { và } y^{\prime \prime}(0)=-10<0$

nên hàm số đạt cực đại tại x = 0

Câu 13

Cho hàm số y=f(x) có đạo hàm $f^{\prime}(x)=(x+1)(x-2)^{2}(x-3)^{3}(x+5)^{4}$ . Hỏi hàm số y =f(x) có mấy điểm cực trị?

A. 2

B. 3

C. 4

D. 5

Lời giải :

$\begin{array}{l}{f^\prime }(x) = (x + 1){(x - 2)^2}{(x - 3)^3}{(x + 5)^4}\\ \Leftrightarrow \left[ \begin{array}{l}x + 1 = 0\\{\left( {x - 2} \right)^2} = 0\\{\left( {x - 3} \right)^3} = 0\\{\left( {x + 5} \right)^4} = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = x\\x = 3\\x = - 5\end{array} \right.\end{array}$

Trong đó x=-1 và x=3 là các nghiệm bội lẻ nên y' đổi dấu khi đi qua x=-1 và x=3. Vậy x=-1 và x=3 là hai cực trị.

Qua các nghiệm bội chẵn x=2 và x=-5 thì y' không đổi dấu nên x=2 và c=-5 không phải cực trị.

Vậy hàm số có hai điểm cực trị.

Câu 14

Cho hàm số y =f(x) . Hàm số y = f'(x) có đồ thị như hình vẽ:

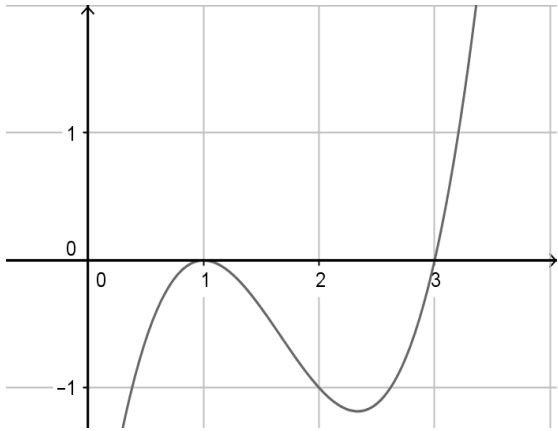
Khẳng định nào sau đây là khẳng định đúng?

A. Hàm số y=f(x) đạt cực đại tại x =1 .

B. Đồ thị hàm số y=f(x) có một điểm cực tiểu.

C. Hàm số y=f(x) đồng biến trên $(-\infty ; 1)$

D. Đồ thị hàm số y=f(x) có hai điểm cực trị

Lời giải :

Trên đồ thị hàm f'(x), khi đi qua x=3 thì y' đổi dấu từ âm sang dương nên x=3 là điểm cực tiểu của hàm số.

Qua x=1 thì y' không đổi sấu nên x=2 không phải cực trị.

Vậy đồ thị hàm số có 1 điểm cực tiểu.

Câu 15

Hàm số $y=x^{3}-3 x^{2}+m x-2$ đạt cực tiểu tại x = 2 khi?

A. $m>0$

B. $m \neq 0$

C. $m<0$

D. $m=0$

Lời giải :

$\begin{array}{l}y^{\prime}=3 x^{2}-6 x+m \\y^{\prime \prime}=6 x-6\end{array}$

Hàm số đạt cực tiểu tại x = 2 khi:

$\left\{\begin{array}{l}y^{\prime}(2)=3.2^{2}-6.2+m=0 \\y^{\prime \prime}(2)=6.2-6>0\end{array} \Leftrightarrow m=0\right.$

Câu 16

Cho hàm số $y=(m-1) x^{3}-3 x^{2}-(m+1) x+3 m^{2}-m+2$ . Để hàm số có cực đại, cực tiểu thì:

A. $m=1$

B. $m \neq 1$

C. $m>1$

D. m tùy ý.

Lời giải :

Hàm số có cực đại, cực tiểu khi $\left\{\begin{array}{l}b^{2}-3 a c>0 \\a \neq 0\end{array} \Leftrightarrow\left\{\begin{array}{l}9+3(m-1)(m+1)>0 \\m-1 \neq 0\end{array} \Leftrightarrow m \neq 1\right.\right.$

Câu 17

Tìm tất cả các giá trị thực của m để hàm số $y=m x^{4}-(m+1) x^{2}+2 m-1$ có 3 điểm cực trị ?

A. $\left[\begin{array}{l}m<-1 \\ m>0\end{array}\right.$

B. $m<-1$

C. $-1

D. $m>-1$

Lời giải :

$y^{\prime}=4 m x^{3}-2(m+1) x=0$

$\Leftrightarrow 2 x\left(2 m x^{2}-m-1\right)=0 \Leftrightarrow\left[\begin{array}{l}x=0 \\2 m x^{2}=m+1\end{array}\right.$

Hàm số có 3 điểm cực trị $\Leftrightarrow m(m+1)>0 \Leftrightarrow\left[\begin{array}{l}m<-1 \\m>0\end{array}\right.$

Câu 18

Tìm tất cả các giá trị thực của tham số m để hàm số: $y=\frac{1}{3} x^{3}+m x^{2}+(m+6) x+m$ có cực đại và cực tiểu .

A. $-2

B. $\left[\begin{array}{l}m<-2 \\ m>3\end{array} .\right.$

C. $\left[\begin{array}{l}m \leq-2 \\ m \geq 3\end{array}\right.$

D. $-2 \leq m \leq 3$

Lời giải :

Ta có $y^{\prime}=x^{2}+2 m x+m+6$

Hàm số có cực đại, cực tiểu $\Leftrightarrow y^{\prime}=0$ có hai nghiệm phân biệt.

$\Leftrightarrow m^{2}-m-6>0 \Leftrightarrow\left[\begin{array}{l}m<-2 \\m>3\end{array}\right.$

Câu 19

Biết giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y=\frac{x^{3}}{3}+2 x^{2}+3 x-4$ trên [-4;0] lần lượt là M và m . Giá trị của M + m bằng

A. $\frac{4}{3}$

B. $-\frac{28}{3}$

C. $4$

D. $-\frac{4}{3}$

Lời giải :

Hàm số $y=\frac{x^{3}}{3}+2 x^{2}+3 x-4$ xác định và liên tục trên [-4;0]

$y^{\prime}=x^{2}+4 x+3, y^{\prime}=0 \Leftrightarrow\left[\begin{array}{l}x=-1(n) \\x=-3(n)\end{array} \right.\\ f(0)=-4, f(-1)=-\frac{16}{3}, f(-3)=-4, f(-4)=-\frac{16}{3}$

Vậy $M=-4, m=-\frac{16}{3} \text { nên } M+m=-\frac{28}{3}$

Câu 20

Đồ thị hàm số sau có bao nhiêu đường tiệm cận $y=\frac{\sqrt{x-2}}{x^{2}-4 x+3} ?$

A. 4

B. 3

C. 2

D. 0

Lời giải :

TXĐ: $D=[2 ;+\infty) \backslash\{3\}$

$\lim \limits_{x \rightarrow+\infty} \frac{\sqrt{x-2}}{x^{2}-4 x+3}=0 \Rightarrow$

y=0 là tiệm cận ngang.

$\lim _{x \rightarrow 3^{+}} \frac{\sqrt{x-2}}{x^{2}-4 x+3}=+\infty ; \lim _{x \rightarrow 3^{-}} \frac{\sqrt{x-2}}{x^{2}-4 x+3}=-\infty \Rightarrow$ x=3 là tiệm cận đứng.

vậy đồ thị hàm số có hai đường tiệm cận.

Câu 21

hàm số phù hợp với bảng biến thiên sau. Phát biểu nào sau đây là đúng

A. Đồ thị hàm số có hai đường tiệm cận ngang là $y=-1 ; y=2$

B. Đồ thị hàm số có 2 đường tiệm cận đứng.

C. Đồ thị hàm số có đường tiệm cận đứng x = -1, tiệm cận ngang y = 2.

D. Đồ thị hàm số không có tiệm cận ngang.

Lời giải :

Dựa vào bảng biến thiên ta có: $\lim \limits_{x \rightarrow+\infty} y=2 ; \lim\limits _{x \rightarrow-\infty} y=-1$ nên đồ thị hàm số có hai đường tiệm cận ngang là $y=2 ; y=-1$

Câu 22

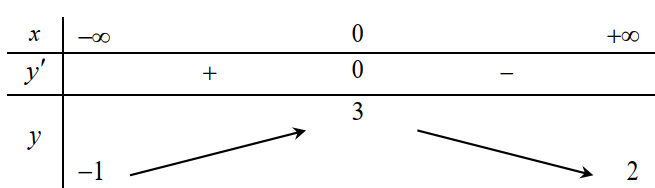
Tìm phương trình tiệm cận đứng của đồ thị hàm số $y=\frac{x-1}{x+1}$

A. x=-1

B. y=1

C. y=-1

D. x=1

Lời giải :

$\mathrm{TXĐ}: D=\mathbb{R} \backslash\{-1\}$

$\lim _{x \rightarrow-1^{+}} y=\lim _{x \rightarrow-1^{+}} \frac{x-1}{x+1}=-\infty \Rightarrow x=-1$ là tiệm cận đứng của đồ thị hàm số.

Câu 23

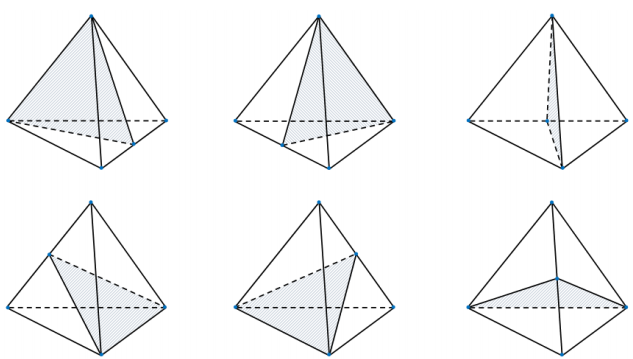
Số mặt phẳng đối xứng của khối tứ diện đều là

A. 7

B. 8

C. 9

D. 6

Lời giải :

Câu 24

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Cạnh bên SA vuông góc với đáy và có độ dài bằng 2a . Thể tích khối tứ diện S.BCD là:

A. $\frac{a^{3}}{4}$

B. $\frac{a^{3}}{8}$

C. $\frac{a^{3}}{6}$

D. $\frac{a^{3}}{3}$

Lời giải :

$S_{\Delta B C D}=\frac{1}{2} S_{A B C D}=\frac{a^{2}}{2} . \text { Suy ra } V_{S . A B C D}=\frac{1}{3} S A . S_{\Delta B C D}=\frac{1}{3} \cdot 2 a \cdot \frac{a^{2}}{2}=\frac{a^{3}}{3}$

Câu 25

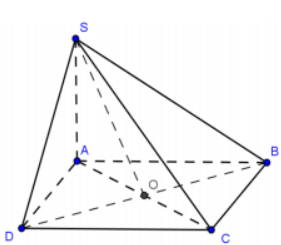
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh 2a . Biết SA vuông góc với mặt phẳng đáy và $S A=a \sqrt{2}$. Tính thể tích khối chóp S.ABO.

A. $\frac{a^{3} \sqrt{2}}{3}$

B. $\frac{2 a^{3} \sqrt{2}}{12}$

C. $\frac{a^{3} \sqrt{2}}{12}$

D. $\frac{4 a^{3} \sqrt{2}}{3}$

Lời giải :

$\begin{array}{l}\text { Ta có: } A C=2 a \cdot \sqrt{2} \Rightarrow O A=O B=\frac{A C}{2}=a \sqrt{2} \Rightarrow S_{O A B}=\frac{1}{2} O A \cdot O B=a^{2} \\\text { Vậy }: V_{S . O A B}=\frac{1}{3} S A . S_{O A B}=\frac{1}{3} \cdot a \sqrt{2} \cdot a^{2}=\frac{\sqrt{2}}{3} \cdot a^{3}\end{array}$

Câu 26

Cho hình chóp tam giác S.ABC với SA , SB , SC đôi một vuông góc và $S A=S B=S C=a$ . Tính thế tích của khối chóp S.ABC.

A. $\frac{1}{2} a^{3}$

B. $\frac{1}{6} a^{3}$

C. $\frac{2}{3} a^{3}$

D. $\frac{1}{3} a^{3}$

Lời giải :

Ta có $V=\frac{1}{3} \cdot S_{S B C} \cdot S A=\frac{1}{3} \cdot \frac{1}{2} \cdot S B \cdot S C \cdot S A=\frac{1}{6} \cdot a^{3}$

Câu 27

Cho hình chóp S.ABCD đáy ABCD là hình vuông có cạnh a và SA vuông góc đáy ABCD và mặt bên (SCD) hợp với đáy một góc 60⁰. Tính thể tích hình chóp S ABCD . .

A. $\frac{a^{3} \sqrt{3}}{3}$

B. $\frac{a^{3} \sqrt{3}}{6}$

C. $a^{3} \sqrt{3}$

D. $\frac{2 a^{3} \sqrt{3}}{3}$

Lời giải :

$\begin{array}{l}\text { Do }\left\{\begin{array}{l}A D \perp C D \\S A \perp C D\end{array} \Rightarrow C D \perp(S D A) \Rightarrow(S C D),(A B C)=\widehat{S D A}\right. \\\text { Khi đó } S A=A D \tan 60^{\circ}=a \sqrt{3} \\\text { Suy ra } V_{S . A B C D}=\frac{1}{3} S A \cdot S_{A B C D}=\frac{a^{3} \sqrt{3}}{3}\end{array}$

Câu 28

Với giá trị nào của thì đẳng thức $\sqrt[2016]{x^{2016}}=-x$ đúng

A. Không có giá trị nào

B. $x\ge 0$

C. x=0

D. $x\le 0$

Lời giải :

Do $\sqrt[2016]{x^{2016}}=|x| \text { nên } \sqrt[2016]{x^{2016}}=-x \Leftrightarrow|x|=-x \text { khi } x \leq 0$

Câu 29

Căn bậc 4 của 3 là

A. $\sqrt[3]{4}$

B. $\sqrt[4]{3}$

C. $-\sqrt[4]{3}$

D. $\pm \sqrt[4]{3}$

Lời giải :

Theo định nghĩa căn bậc n của số b : Cho số thực n và số nguyên dương b $(n \geq 2)$ .

Số a được gọi là căn bậc n của số b nếu $a^{n}=b$

Nếu n chẵn và b>0 Có hai căn trái dấu, kí hiệu giá trị dương là $\sqrt[n]{b}$ , còn giá trị âm kí hiệu là $-\sqrt[n]{b}$ . Nên có hai căn bậc 4 của 3 là $\pm \sqrt[4]{3}$

Câu 30

Với giá trị nào của thì biểu thức $\left(4-x^{2}\right)^{\frac{1}{3}}$ có nghĩa

A. $x \geq 2$

B. $-2

C. $x \leq-2$

D. Không có giá trị x nào.

Lời giải :

ĐKXĐ: $4-x^{2}>0 \Leftrightarrow-2<x<2$

Câu 31

So sánh hai số m và n nếu $3,2^{m}<3,2^{n}$ thì:

A. m>n

B. m=n

C. m

D. Không so sánh được.

Lời giải :

$\text { Do } 3,2>1 \text { nên } 3,2^{m}<3,2^{n} \Leftrightarrow m<n$

Câu 32

Cho $a=1+2^{-x}, b=1+2^{x}$ . Biểu thức biểu diễn b theo a là:

A. $\frac{a-2}{a-1}$

B. $\frac{a-1}{a}$

C. $\frac{a+2}{a-1}$

D. $\frac{a}{a-1}$

Lời giải :

$\begin{aligned}&\text { Ta có: } a=1+2^{-x}>1, \forall x \in \mathbb{R} \text { nên } 2^{x}=\frac{1}{a-1}\\&\text { Do đó: } b=1+\frac{1}{a-1}=\frac{a}{a-1}\end{aligned}$

Câu 33

Tập xác định của hàm số $y=\log _{0,5}(x+1)$ là:

A. $D=(-1 ;+\infty)$

B. $D=\mathbb{R} \backslash\{-1\}$

C. $D=(0 ;+\infty)$

D. $(-\infty ;-1)$

Lời giải :

ĐKXĐ: $x+1>0 \Leftrightarrow x>-1$

Câu 34

Cho hàm số $y=3^{\frac{x}{2}}$có đồ thị (C). Hàm số nào sau đây có đồ thị đối xứng với qua đường thẳng y=x

A. $y=\log _{\sqrt{3}} x$

B. $y=\log _{3} x^{2}$

C. $y=\log _{3}\left(\frac{x}{2}\right)$

D. $y=\frac{1}{2} \log _{3} x$

Lời giải :

Ta có $y=3^{\frac{x}{2}}=(\sqrt{3})^{x}$

dựa vào lý thuyết Hai hàm số $y=a^{x} \text { và } y=\log _{a} x$ có đồ thị đối xứng nhau qua đường phân giác của góc phần tư thứ nhất y=x ''

Vậy chọn A

Câu 35

Phương trình $3^{x^{3}-9 x+4}=81$ có mấy nghiệm?

A. 1

B. 2

C. 3

D. 4

Lời giải :

Ta có $3^{x^{3}-9 x+4}=81=3^{4} \Leftrightarrow x^{3}-9 x+4=4 \Leftrightarrow x\left(x^{2}-9\right)=0 \Leftrightarrow x \in\{0 ;\pm 3\}$

Vậy phương trình có 3 nghiệm.

Câu 36

Cho phương trình $4.4^{x}-9.2^{x+1}+8=0$ . Gọi $x_1; x_2$ là hai nghiệm của phương trình trên. Khi đó, tích $x_1. x_2$ bằng:

A. -1

B. 2

C. -2

D. 1

Lời giải :

Đặt $t=2^{x}(t>0)$, khi đó phương trình đã cho tương đương với

$4 t^{2}-18 t+8=0 \Leftrightarrow\left[\begin{array}{l}t=4 \\t=\frac{1}{2}\end{array} \Leftrightarrow\left[\begin{array}{l}x_{1}=2 \\x_{2}=-1\end{array}\right.\right.$

Vậy $x_{1} \cdot x_{2}=-1.2=-2$

Câu 37

Tổng các nghiệm không âm của phương trình $\log _{\sqrt{3}} x-\log _{3}\left(2 x^{2}-4 x+3\right)=0$ là:

A. 1

B. 2

C. 4

D. 3

Lời giải :

$\begin{aligned}&\text { Điều kiện } x>0\\&\log _{\sqrt{3}} x-\log _{3}\left(2 x^{2}-4 x+3\right)=0 \Leftrightarrow 2 \log _{3} x-\log _{3}\left(2 x^{2}-4 x+3\right)=0 \Leftrightarrow \log _{3} x^{2}=\log _{3}\left(2 x^{2}-4 x+3\right)\\&\Leftrightarrow x^{2}=2 x^{2}-4 x+3 \Leftrightarrow x^{2}-4 x+3=0 \Leftrightarrow\left[\begin{array}{l}x_{1}=1 \\x_{2}=3\end{array} \Rightarrow x_{1}+x_{2}=4\right.\end{aligned}$

Câu 38

Với giá trị m bằng bao nhiêu thì phương trình $\log _{2+\sqrt{3}}(m x+3)+\log _{2-\sqrt{3}}\left(m^{2}+1\right)=0$ có nghiệm là -1 ?

A. $\begin{aligned}&\left[\begin{array}{l}m=1 \\m=-1\end{array}\right.\end{aligned}$

B. $\left[\begin{array}{l}m=1 \\m=-2\end{array}\right.$

C. $m<3$

D. $m>3$

Lời giải :

Thay x =-1vào phương trình ta có

$\begin{array}{l} \log _{2+\sqrt{3}}(-m+3)+\log _{2-\sqrt{3}}\left(m^{2}+1\right)=0 \Leftrightarrow \log _{2+\sqrt{3}}(-m+3)+\log _{(2+\sqrt{3})^{-1}}\left(m^{2}+1\right)=0 \\ \Leftrightarrow \log _{2+\sqrt{3}}(-m+3)-\log _{(2+\sqrt{3})}\left(m^{2}+1\right)=0 \Leftrightarrow \log _{2+\sqrt{3}}(-m+3)=\log _{(2+\sqrt{3})}\left(m^{2}+1\right) \\ \Leftrightarrow-m+3=m^{2}+1 \Leftrightarrow m^{2}+m-2=0 \Leftrightarrow\left[\begin{array}{l} m=1 \\ m=-2 \end{array}\right. \end{array}$

Câu 39

Trong không gian Oxyz, cho $A(1 ; 0 ; 1), B(0;1;-1)$. Tính độ dài AB

A. $\sqrt 3$

B. $\sqrt 2$

C. 1

D. $2\sqrt 2$

Lời giải :

$AB=\sqrt {(x_A-x_B)^2+(y_A-y_B)^2+(y_A-y_B)^2}=\sqrt {1+1+1}=\sqrt 3$

Câu 40

Tập nghiệm của phương trìnhlog $\log _{\sqrt{3}}|x-1|=2$ là:

A. $\{3\}$

B. $\{-3 ; 4\}$

C. $\{-2 ;-3\}$

D. $\{4 ;-2\}$

Lời giải :

$\log _{\sqrt{3}}|x-1|=2 \Leftrightarrow|x-1|=3 \Leftrightarrow\left[\begin{array}{l}x=4 \\x=-2\end{array}\right.$

Kết quả

Nộp bài

Kết quả

Hoàn thành

Đề thi thử giữa học kỳ 1 môn Toán lớp 12 online - Mã đề 11

Trở thành Membership ngay

MEGA-AI phản hồi

Đăng nhập