Đề thi thử học kỳ 1 môn Toán lớp 11 online - Mã đề 16

Ta có:

\(\tan 3x = \tan (\dfrac{\pi }{3} - 2x)\\\Leftrightarrow 3x = \dfrac{\pi }{3} - 2x + k\pi \;\left( {k \in \mathbb{Z}} \right)\)

\( \Leftrightarrow 5x = \dfrac{\pi }{3} + k\pi \left( {k \in \mathbb{Z}} \right)\\\Leftrightarrow x = \dfrac{\pi }{{15}} + k\dfrac{\pi }{5}\;\left( {k \in \mathbb{Z}} \right)\)

Ta có: \(\dfrac{{\cos x + 2\sin x + 3}}{{2\cos x - \sin x + 4}} = m \)

\(\Leftrightarrow \cos x + 2\sin x + 3 = m\left( {2\cos x - \sin x + 4} \right)\)

\(\Leftrightarrow \left( {2m - 1} \right)\cos x - \left( {m + 2} \right)\sin x = 3 - 4m\)

Điều kiện có nghiệm: \({\left( {2m - 1} \right)^2} + {\left( {m + 2} \right)^2} \ge {\left( {3 - 4m} \right)^2}\)

\(\Leftrightarrow 4{m^2} - 4m + 1 + {m^2} + 4m + 4\ge 9 - 24m + 16{m^2}\)

\( \Leftrightarrow 11{m^2} - 24m + 4 \le 0\\\Leftrightarrow \dfrac{2}{{11}} \le m \le 2.\)

Ta có: \(\sin x + \sqrt 3 \cos x = \sqrt 2 \)

\(\begin{array}{l}\Leftrightarrow \frac{1}{2}\sin x + \frac{{\sqrt 3 }}{2}\cos x = \frac{{\sqrt 2 }}{2}\\\Leftrightarrow \cos \frac{\pi }{3}\sin x + \sin \frac{\pi }{3}\cos x = \frac{{\sqrt 2 }}{2}\end{array}\)

\(\\ \Leftrightarrow \sin \left( {x + \dfrac{\pi }{3}} \right) = \dfrac{{\sqrt 2 }}{2}\\ \Leftrightarrow \sin \left( {x + \dfrac{\pi }{3}} \right) = \sin \dfrac{\pi }{4} \\ \Leftrightarrow \left[ \begin{array}{l}x + \dfrac{\pi }{3} = \dfrac{\pi }{4} + k2\pi \\x + \dfrac{\pi }{3} = \pi - \dfrac{\pi }{4} + k2\pi \end{array} \right.\,\left( {k \in \mathbb{Z}} \right)\\ \Leftrightarrow \left[ \begin{array}{l}x = - \dfrac{\pi }{{12}} + k2\pi \\x = \dfrac{{5\pi }}{{12}} + k2\pi \end{array} \right.\,\left( {k \in \mathbb{Z}} \right)\)

+ Hàm số y = sin x, y = cos x có chu kỳ là \(T = 2\pi \)

+ Hàm số y = tan x, y = cot x có chu kì là \(T = \pi \)

Ta có: 

\(2{\sin ^2}x + 5\sin x - 3 = 0 \\\Leftrightarrow \left( {2\sin x - 1} \right)\left( {\sin x + 3} \right) = 0\)

\(\Leftrightarrow \sin x = \dfrac{1}{2} \\\Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{6} + k2\pi \\x = \dfrac{{5\pi }}{6} + k2\pi \end{array} \right.\,\left( {k \in \mathbb{Z}} \right)\)

Nghiệm dương bé nhất của phương trình là \(x = \dfrac{\pi }{6}.\)

Hàm số y = cot x có đồ thị không là đường hình sin.

\(y = f(x) = 2\cot (2x - \dfrac{\pi }{3}) + 1\\= \dfrac{{2\cos (2x - \dfrac{\pi }{3})}}{{\sin (2x - \dfrac{\pi }{3})}} + 1\)

ĐKXĐ: \(\sin \left( {2x - \dfrac{\pi }{3}} \right) \ne 0 \)

\(\Leftrightarrow \left( {2x - \dfrac{\pi }{3}} \right) \ne k\pi \;\left( {k \in \mathbb{Z}} \right)\)

\(\Leftrightarrow x \ne \dfrac{\pi }{6} + k\dfrac{\pi }{2}\;\left( {k \in \mathbb{Z}} \right)\)

Ta có: \(\tan (x - \dfrac{\pi }{2}) = \sqrt 3 \)

\(\Leftrightarrow \tan (x - \dfrac{\pi }{2}) = \tan \dfrac{\pi }{3}\\\Leftrightarrow x - \dfrac{\pi }{2} = \dfrac{\pi }{3} + k\pi \;\left( {k \in \mathbb{Z}} \right)\\\Leftrightarrow x = \dfrac{{5\pi }}{6} + k\pi \;\left( {k \in \mathbb{Z}} \right)\)

Đáp án A: TXĐ: D=R.

Ta có: 

\(\begin{array}{l}y\left( { - x} \right) = \sin \left| { - 2016x} \right| + \cos \left( { - 2017x} \right)\\= \sin 2016x + \cos 2017x = y\left( x \right)\end{array}\)

Hàm số \(y = \sin \left| {2016x} \right| + c{\rm{os}}2017x\) là hàm số chẵn.

Ta có: \(\sin x \in \left[ { - 1;1} \right] \)

\(\begin{array}{l}\Rightarrow - 1 \le \sin x \le 1\\\Rightarrow - 3 \le 3\sin x \le 3\\\Rightarrow - 2 \le 3\sin x + 1 \le 4\end{array}\)

Ta có:

\(\cot x = \sqrt 3 \Leftrightarrow x = \dfrac{\pi }{6} + k\pi \;\left( {k \in \mathbb{Z}} \right)\)

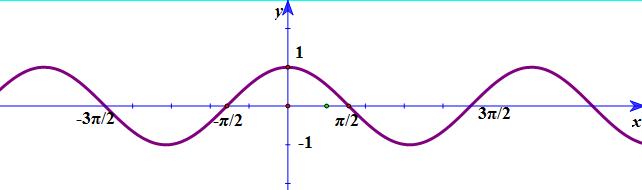
Đồ thị hình bên là của hàm số y = cos x

Một số gồm 4 chữ số phân biệt lập thành từ các chữ số A = {1; 2; 3; …; 9} có dạng:

\(\overline {{a_1}{a_2}{a_3}{a_4}} \) với \({a_i} \in A,i = \overline {1,4}\) và \({a_i} \ne {a_j},i \ne j.\)

Do \(\overline {{a_1}{a_2}{a_3}{a_4}}\) không vượt quá 2011 nên \({a_1} = 1\): có 1 cách chọn.

Mặt khác, \(\overline {{a_1}{a_2}{a_3}{a_4}} \) là số chẵn nên \({a_4} \in \left\{ {2;4;6;8} \right\}:\) có \(C_4^1\) cách chọn.

Khi đó, \({a_3}\) có \(C_7^1\) cách chọn.

            \({a_2}\) có \(C_6^1\) cách chọn.

Số cách chọn là \(1.C_4^1.C_7^1.C_6^1 = 168\)

Ta có

\(\begin{array}{c}{\left( {2x - 1} \right)^{10}} = C_{10}^0{\left( {2x} \right)^{10}} + C_{10}^1{\left( {2x} \right)^9}\left( { - 1} \right) + ... + C_{10}^{10}{\left( { - 1} \right)^{10}}\\ = C_{10}^0{2^{10}}{x^{10}} + C_{10}^1{2^9}{x^9}\left( { - 1} \right) + C_{10}^2{2^8}{\left( { - 1} \right)^2}{x^8} + ... + C_{10}^{10}{\left( { - 1} \right)^{10}}\end{array}\)

Do đó hệ số của số hạng chứa x⁸ là \(C_{10}^2{2^8}{\left( { - 1} \right)^2} = 11520\)

Cứ 2 đội nếu đá 2 trận lượt đi và 2 trận lượt về sẽ có 4 trận đấu diễn ra.

Vậy số trận đấu được sắp xếp khi có 10 đội là \(4.C_{10}^2 = 180\).

Số cách lấy ra lần lượt 2 bi từ hộp là \(C_{10}^1.C_9^1 = 90 \Rightarrow n\left( \Omega \right) = 90.\)

Số cách lấy ra lần lượt 1 bi xanh và 1 bi đỏ là \(C_4^1.C_6^1 = 24 \Rightarrow n\left( A \right) = 24.\)

Xác suất để lấy ra 1 bi xanh và 1 bi đỏ là \(P\left( A \right) = \dfrac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \dfrac{{24}}{{90}} = \dfrac{4}{{15}}\)

Vì để 2 bạn học sinh nam ngồi gần nhau nên ta coi sắp xếp này là 1 chỗ ngồi. Cùng với 3 học sinh nữ ta có 4 chỗ.

Nên có 4! cách xếp chỗ.

Mà trong 2 học sinh nam có 2! cách sắp.

Vậy ta có 4!.2! = 48 cách sắp.

Gọi A là tập hợp cách chọn 4 học sinh trong 12 học sinh.

Gọi B là tập hợp cách chọn 4 số học sinh mà mỗi lớp có ít nhất một em.

Gọi C là tập hợp cách chọn thỏa mãn yêu cầu đề bài.

Khi đó \(A = B \cup C;B \cap C = \emptyset .\)

Theo quy tắc cộng ta có: 

\(n\left( A \right) = n\left( B \right) + n\left( C \right) \Rightarrow n\left( C \right) = n\left( A \right) - n\left( B \right)\)

Ta có \(n\left( A \right) = C_{12}^4 = 495\)

Để tính n(B), ta nhận thấy sẽ chọn mỗi lớp 2 học sinh, còn 2 lớp còn lại mỗi lớp 1 học sinh.

Vì thế theo quy tắc cộng và phép nhân, ta có

\(n\left( B \right) = C_5^2C_4^1C_3^1 + C_5^1C_4^2C_3^1 + C_5^1C_4^1C_3^2 \)

= 120 + 90 + 60 = 270

\(\Rightarrow n\left( C \right) = n\left( A \right) - n\left( B \right) = 495 - 270 = 225\)

Ta có \(n\left( \Omega \right) = C_{52}^1 = 52.\)

Số cách rút để được lá 10 hay lá át là \(n\left( A \right) = C_8^1 = 8.\)

Xác suất cần có là:

\(P\left( A \right) = \dfrac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \dfrac{8}{{52}} = \dfrac{2}{{13}}\)

Tổng số bông hoa hiện có là: 3 + 3 + 4 = 10

Số cách chọn tùy ý ra 7 bông hoa là: \(C_{10}^7 = 120.\)

Số cách chọn nhóm đồng ca có 3 nữ là: \(C_5^3.C_{10}^5 = 2520.\)

Số cách chọn nhóm đồng ca có 4 nữ là: \(C_5^4.C_{10}^4 = 1050.\)

Số cách chọn nhóm đồng ca có 5 nữ là: \(C_5^5.C_{10}^3 = 120.\)

Vậy số cách chọn nhóm đồng ca có ít nhất 3 nữ là: \(2520 + 1050 + 120 = 3690\)

Ta có một số chia hết cho 3 khi và chỉ khi tổng các chữ số chia hết cho 3.

Trong tập hợp A có các tập số con gồm 4 chữ số khác nhau chia hết cho 3 là:

\(\begin{array}{l}\left\{ {0;1;2;3} \right\},\left\{ {0;1;2;6} \right\},\left\{ {0;2;3;4} \right\},\left\{ {0;3;4;5} \right\};\\\left\{ {1;2;4;5} \right\},\left\{ {1;2;3;6} \right\},\left\{ {1;3;5;6} \right\}.\end{array}\)

Vậy số các số cần lập là: \(4\left( {4! - 3!} \right) + 3.4! = 144\)

Ta có \(C_n^1 = n\)

Ta có

\(\begin{array}{c}{\left( {3{x^2} - y} \right)^{10}} = C_{10}^0{\left( {3{x^2}} \right)^{10}} + C_{10}^1{\left( {3{x^2}} \right)^9}\left( { - y} \right) + ... + C_{10}^{10}{\left( { - y} \right)^{10}}\\ = C_{10}^0{3^{10}}{x^{20}} + C_{10}^1{3^9}{x^{18}}\left( { - y} \right) + ... + C_{10}^{10}{\left( { - y} \right)^{10}}\end{array}\)

Vậy hệ số của số hạng chính giữa là: \(- C_{10}^5{3^5}\)

(C) có tâm \(I\left( {2; - 5} \right)\) bán kính \(R = \sqrt 5 \).

Gọi \(I' = {Q_{\left( {O;{{180}^0}} \right)}}\left( I \right)\) thì I' đối xứng với I qua O

\(\Rightarrow \left\{ \begin{array}{l}{x_{I'}} = - {x_I} = - 2\\{y_{I'}} = - {y_I} = 5\end{array} \right. \Rightarrow I'\left( { - 2;5} \right)\)

Vậy \(\left( {C'} \right):{\left( {x + 2} \right)^2} + {\left( {y - 5} \right)^2} = 5\)

(C) có tâm \(I\left( {3; - 2} \right)\) và bán kính R = 3.

\(\begin{array}{l}I' = {T_{\overrightarrow v }}\left( I \right) \Rightarrow \overrightarrow {II'} = \overrightarrow v \\ \Rightarrow \left\{ \begin{array}{l}{x_{I'}} = {x_I} + 3 = 3 + 3 = 6\\{y_{I'}} = {y_I} - 2 = - 2 - 2 = - 4\end{array} \right.\\ \Rightarrow I'\left( {6; - 4} \right)\end{array}\)

Vậy \(\left( {C'} \right):{\left( {x - 6} \right)^2} + {\left( {y + 4} \right)^2} = 9\)

Sử dụng chú ý a trang 21 SGK hình học 11:

Nếu một phép dời hình biến tam giác ABC thành tam giác A’B’C’ thì nó cũng biến trọng tâm, trực tâm, tâm các đường tròn nội tiếp, ngoại tiếp của tam giác ABC tương ứng thành trọng tâm, trực tâm, tâm các đường tròn nội tiếp, ngoại tiếp của tam giác A’B’C’.

Vậy cả 3 mệnh đề đều đúng.

Gọi G là trọng tâm tam giác ABC. Khi đó

\(\overrightarrow {GN} = - \frac{1}{2}\overrightarrow {GA} \Rightarrow {V_{\left( {G, - \frac{1}{2}} \right)}}\left( A \right) = N\)

\(\overrightarrow {GP} = - \frac{1}{2}\overrightarrow {GB} \Rightarrow {V_{\left( {G, - \frac{1}{2}} \right)}}\left( B \right) = P\)

\(\overrightarrow {GM} = - \frac{1}{2}\overrightarrow {GC} \Rightarrow {V_{\left( {G, - \frac{1}{2}} \right)}}\left( C \right) = M\)

Vậy \({V_{\left( {G, - \frac{1}{2}} \right)}}\left( {\Delta ABC} \right) = \Delta NPM\)

(C) có tâm O(0;0) bán kính R = 2.

Gọi d’ là đường thẳng đi qua O và vuông góc với d.

\( \overrightarrow {{n_d}} = \left( {1; - 1} \right)\) là VTPT của d nên \(\overrightarrow {{n_{d'}}} = \left( {1;1} \right)\) là VTPT của d’.

Do đó d':x + y = 0.

M là giao điểm của d’ và (C) nên tọa độ của M thỏa mãn hệ phương trình:

\(\begin{array}{l}\left\{ \begin{array}{l}x + y = 0\\{x^2} + {y^2} = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = - x\\{x^2} + {x^2} = 4\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}y = - x\\2{x^2} = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = - x\\{x^2} = 2\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}y = - x\\x = \pm \sqrt 2 \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = \sqrt 2 ,y = - \sqrt 2 \\x = - \sqrt 2 ,y = \sqrt 2 \end{array} \right.\end{array}\)

Xét \({M_1}\left( {\sqrt 2 ; - \sqrt 2 } \right)\) có \(d\left( {{M_1};d} \right) = \frac{{\left| {\sqrt 2 + \sqrt 2 + 2} \right|}}{{\sqrt {{1^2} + {{\left( { - 1} \right)}^2}} }} = 2 + \sqrt 2 \)

Xét \({M_2}\left( { - \sqrt 2 ;\sqrt 2 } \right)\) có \(d\left( {{M_2};d} \right) = \frac{{\left| { - \sqrt 2 - \sqrt 2 + 2} \right|}}{{\sqrt {{1^2} + {{\left( { - 1} \right)}^2}} }} = 2 - \sqrt 2 \)

Vì \(d\left( {{M_1};d} \right) > d\left( {{M_2};d} \right)\) nên \(M \equiv {M_1}\left( {\sqrt 2 ; - \sqrt 2 } \right)\).

\({V_{\left( {O;\sqrt 2 } \right)}}\left( M \right) = M'\\ \Rightarrow \left\{ \begin{array}{l}{x_{M'}} = \sqrt 2 {x_M} = \sqrt 2 .\sqrt 2 = 2\\{y_{M'}} = \sqrt 2 {y_M} = \sqrt 2 .\left( { - \sqrt 2 } \right) = - 2\end{array} \right.\).

Gọi phương trình (C) là \({x^2} + {y^2} - 2ax - 2by + c = 0\)

\(A,B,C \in \left( C \right)\)

\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}{3^2} + {4^2} - 6a - 8b + c = 0\\{\left( { - 3} \right)^2} + {\left( { - 2} \right)^2} + 6a + 4b + c = 0\\{9^2} + {\left( { - 2} \right)^2} - 18a + 4b + c = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} - 6x - 8b + c = - 25\\6a + 4b + c = - 13\\ - 18a + 4b + c = - 85\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}a = 3\\b = - 2\\c = - 23\end{array} \right.\\ \Rightarrow \left( C \right):{x^2} + {y^2} - 6x + 4y - 23 = 0\end{array}\)

(C ) có tâm \(I\left( {3; - 2} \right)\) bán kính \(R = \sqrt {{3^2} + {{\left( { - 2} \right)}^2} - \left( { - 23} \right)} = 6\)

Gọi \(I' = {T_{\overrightarrow v }}\left( I \right)\Rightarrow \left\{ \begin{array}{l}{x_{I'}} = 3 + 3 = 6\\{y_{I'}} = - 2 + 5 = 3\end{array} \right. \Rightarrow I'\left( {6;3} \right)\)

\(I'' = {V_{\left( {O; - \frac{1}{3}} \right)}}\left( {I'} \right)\\\Rightarrow \left\{ \begin{array}{l}{x_{I''}} = - \frac{1}{3}{x_{I'}} = - \frac{1}{3}.6 = - 2\\{y_{I''}} = - \frac{1}{3}{y_{I'}} = - \frac{1}{3}.3 = - 1\end{array} \right.\\ \Rightarrow I''\left( { - 2; - 1} \right)\)

(C’) có tâm \(I''\left( { - 2; - 1} \right)\) bán kính \(R'' = \left| { - \frac{1}{3}} \right|R = \frac{1}{3}.6 = 2\) nên có phương trình:

\(\left( {C'} \right):{\left( {x + 2} \right)^2} + {\left( {y + 1} \right)^2} = 4\)

Phép tịnh tiến biến đường thẳng thành đường thẳng song song hoặc trùng với nó nên B sai.

Phép dời hình biến đoạn thẳng thành đoạn thẳng bằng nó nên A sai.

Lấy \(A\left( {5;0} \right) \in d\), gọi \(A' = {Q_{\left( {O,\frac{\pi }{2}} \right)}}\left( A \right)\) thì \(A'\left( {0;5} \right)\).

Ta có: \(\overrightarrow {{n_d}} = \left( {1; - 2} \right)\), mà \(d' \bot d\ \Rightarrow \overrightarrow {{n_{d'}}} = \left( {2;1} \right)\).

Vậy \(d':2\left( {x - 0} \right) + 1\left( {y - 5} \right) = 0\Leftrightarrow 2x + y - 5 = 0\)

(C ) có bán kính R = 6 nên (C’) có bán kính R' = kR = 3.6 = 18

Gọi I(a;b)

\(M' = {V_{\left( {I; - \frac{1}{2}} \right)}}\left( M \right) \Leftrightarrow \overrightarrow {IM'} = - \frac{1}{2}\overrightarrow {IM} \)

\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l} - 3 - a = - \frac{1}{2}\left( {4 - a} \right)\\5 - b = - \frac{1}{2}\left( {6 - b} \right)\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} - 6 - 2a = - 4 + a\\10 - 2b = - 6 + b\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} - 2 = 3a\\16 = 3b\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - \frac{2}{3}\\b = \frac{{16}}{3}\end{array} \right.\\ \Rightarrow I\left( { - \frac{2}{3};\frac{{16}}{3}} \right)\end{array}\)

\(A' = {V_{\left( {I;2} \right)}}\left( A \right) \Leftrightarrow \overrightarrow {IA'} = k\overrightarrow {IA} \)

\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}{x_{A'}} - 3 = 2\left( {1 - 3} \right)\\{y_{A'}} - \left( { - 1} \right) = 2\left( {2 - \left( { - 1} \right)} \right)\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{x_{A'}} - 3 = - 4\\{y_{A'}} + 1 = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_{A'}} = - 1\\{y_{A'}} = 5\end{array} \right.\\ \Rightarrow A'\left( { - 1;5} \right)\end{array}\)

+) A sai. Trong trường hợp 2 đường thẳng cắt nhau thì chúng chỉ có 1 điểm chung.

+) B và C sai. Hai đường thẳng song song khi và chỉ khi chúng đồng phằng và không có điểm chung.

+) A và B sai. Hai đường thẳng cùng song song với đường thẳng thứ ba thì song song hoặc trùng nhau.

+) D sai. Hai đường thẳng cùng song song với đường thẳng thứ ba thì chúng đồng phẳng.

Vì a và b chéo nhau nên bốn điểm A, B, C, D không đồng phẳng, từ đó dẫn đến AD và BC chéo nhau.

Ta có MP cắt NQ tại I

\(\Rightarrow \left\{ \begin{array}{l}I \in MP\\I \in NQ\end{array} \right. \Rightarrow \left\{ \begin{array}{l}I \in \left( {ABD} \right)\\I \in \left( {CBD} \right)\end{array} \right..\)

\(\Rightarrow I \in \left( {ABD} \right) \cap \left( {CBD} \right)\)

\(\Rightarrow I \in BD\)

Vậy I, B, D thẳng hàng.