Đề thi thử học kỳ 1 môn Toán lớp 11 online - Mã đề 14
Vui lòng cài đặt đề thi trước khi làm bài
Giải phương trình ${\tan ^2}3x - 1 = 0$.
Tính giá trị biểu thức $P = {\sin ^2}{45^0} - \cos {60^0}$.
Phương trình nào sau đây có nghiệm?
Phương trình nào sau đây vô nghiệm?
Hàm số nào sau đây xác định với mọi $x \in \mathbb{R}$.
Số nghiệm của phương trình $2\cos x + \sqrt 2 = 0$ trên khoảng $\left( { - 6;6} \right)$ là bao nhiêu?
Hàm số nào sau đây không phải là hàm số chẵn, cũng không phải là hàm số lẻ.
Mệnh đề nào sau đây sai?
GTNN và GTLN của hàm số $y = 4\sqrt {\sin x + 3} - 1$ lần lượt là bao nhiêu?
Nghiệm đặc biệt nào sau đây là sai?
Số nghiệm của phương trình $\sin 2x = \dfrac{{\sqrt 3 }}{2}$ trong $\left( {0;3\pi } \right)$ là mấy?
Tìm tổng các nghiệm của phương trình $2\cos \left( {x - \dfrac{\pi }{3}} \right) = 1$ trên $\left( { - \pi ;\pi } \right)$.
Với $\dfrac{{\left( {n + 1} \right)!}}{{\left( {n - 1} \right)!}} = 72$ thì giá trị của n là bao nhiêu?
Một cuộc họp có 13 người, lúc ra về mỗi người đều bắt tay người khác một lần, riêng chủ tọa chỉ bắt tay ba người. Hỏi có bao nhiêu cái bắt tay?
Trong tủ sách có tất cả 10 cuốn sách. Hỏi có bao nhiêu cách sắp xếp sao cho quyển thứ nhất ở kề quyển thứ 2?
Trong khai triển ${(x - \sqrt y )^{16}}$, tổng hai số hạng cuối là giá trị nào dưới đây?
Từ thành phố A có 10 con đường đến thành phố B, từ thành phố A có 9 con đường đến thành phố C, từ B đến D có 6 con đường, từ C đến D có 11 con đường và không có con đường nào nối B với C. Hỏi có bao nhiêu cách đi từ A đến D.
Trong khai triển ${(2a - 1)^6}$, tổng ba số hạng đầu là bao nhiêu?
Cho đa giác đều ${A_1}{A_2}...{A_{2n}}$ nội tiếp đường tròn tâm O. Biết rằng số tam giác có đỉnh là 3 trong 2n điểm ${A_1},{A_2},...,{A_{2n}}$ gấp 20 lần so với số hình chữ nhật có đỉnh là 4 trong 2n điểm ${A_1},{A_2},...,{A_{2n}}$. Tìm n?
Một thầy giáo có 5 cuốn sách toán, 6 cuốn sách văn, 7 cuốn sách Anh văn và các cuốn sách đôi một khác nhau. Thầy giáo muốn tặng 6 cuốn sách cho 6 học sinh. Hỏi thầy giáo có bao nhiêu cách tặng nếu thầy giáo muốn sau khi tặng xong mỗi thể loại còn lại ít nhất 1 cuốn?
Trong khai triển ${\left( {8{a^2} - \dfrac{1}{2}b} \right)^6}$ hệ số của số hạng chứa ${a^6}{b^3}$ là bao nhiêu?
Một lớp có 33 học sinh, trong đó có 7 nữ. Cần chia lớp thành 3 tổ, tổ 1 có 10 học sinh, tổ 2 có 11 học sinh, tổ 3 có 12 học sinh sao cho trong mỗi tổ có ít nhất 2 học sinh nữ. Hỏi có bao nhiêu cách chia như vậy?
Một hội nghị bàn tròn có các phái đoàn gồm 3 người Anh, 5 người Pháp, 7 người Mỹ. Hỏi có bao nhiêu cách xếp chỗ ngồi cho các thành viên, sao cho những người có cùng quốc tịch thì ngồi gần nhau?
Cho các số 1,2,3,4,5,6,7. Số các số tự nhiên gồm 5 chữ số lấy từ 7 chữ số trên sao cho chữ số đầu tiên bằng 3 là bao nhiêu?
Cho P, Q cố định và phép tịnh tiến T biến điểm M bất kỳ thành M2 sao cho $\overrightarrow {M{M_2}} = 2\overrightarrow {PQ} $. Chọn kết luận đúng?
Trong mặt phẳng Oxy, phép tịnh tiến theo vectơ $\vec v = (1;3)$ biến điểm A (1;2) thành điểm nào trong các điểm sau đây ?
Giả sử rằng qua phép đối xứng trục ${{\rm{D}}_a}$ ( a là trục đối xứng ), đường thẳng d biến thành đường thẳng d'. Hãy chọn câu sai trong các câu sau ?
Phép quay ${Q_{(O;\varphi )}}$ biến điểm A thành M. Khi đó
(I): O cách đều A và M.
(II): O thuộc đường tròn đường kính AM.
(III): O nằm trên cung chứa góc $\varphi $ dựng trên đoạn AM.
Trong các câu trên, câu đúng là:
Cho M ( 3;4) . Tìm ảnh của điểm M qua phép quay tâm O góc quay ${30^0}$.
Trong mặt phẳng Oxy cho đường thẳng d có phương trình: x + y - 2 = 0. Hỏi phép dời hình có được bằng cách thực hiện liên tiếp phép đối xứng tâm O và phép tịnh tiến theo vectơ $\vec v = \left( {3;2} \right)$ biến đường thẳng d thành đường thẳng nào trong các đường thẳng sau ?
Cho tam giác ABC với trọng tâm G. Gọi A',B',C' lần lượt là trung điểm của các cạnh BC, AC, AB của tam giác ABC. Khi đó phép vị tự nào biến tam giác A'B'C' thành tam giác ABC?
Trong mặt phẳng với hệ trục tọa độ Oxy. Cho hai đường tròn (C), (C') trong đó (C') có phương trình: ${\left( {x + 2} \right)^2} + {\left( {y + 1} \right)^2} = 9$. Gọi V là phép vị tự tâm I (1;0) tỉ số k = 3 biến đường tròn (C) thành (C'). Khi đó phương trình của (C) là phương trình nào dưới đây?
Kể tên các phép biến hình biến đường thẳng thành đường thẳng song song hoặc trùng với nó.
Trong mặt phẳng với hệ trục tọa độ Oxy cho A ( -2;-3), B ( 4;1). Phép đồng dạng có tỉ số $k = {1 \over 2}$ biến điểm A thành A', biến điểm B thành B'. Khi đó độ dài A'B' bằng bao nhiêu?
Cho đường thẳng d có phương trình x - y + 4 = 0. Hỏi trong các đường thẳng sau đường thẳng nào có thể biến thành d qua một phép đối xứng tâm?
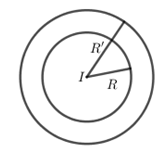
Cho hai đường tròn tâm $\left( {I;R} \right)$ và $\left( {I;R'} \right)\,\,\left( {R \ne R'} \right)$. Có bao nhiêu phép vị tự biến đường tròn tâm $\left( {I;R} \right)$ thành đường tròn $\left( {I;R'} \right)?$
Cho hình chóp S.ABCD, hai đường thẳng AC và BD cắt nhau tại điểm M, hai đường thẳng AB và CD cắt nhau tại điểm N. Giao tuyến của mặt phẳng (SAB) và mặt phẳng (SCD) là đường thẳng nào trong các đường thẳng sau đây ?
Tìm mệnh đề đúng trong các mệnh đề sau.
Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng. Gọi $O,{O_1}$ lần lượt là tâm của ABCD, ABEF. Lấy M là trung điểm của CD. Hỏi khẳng định nào sau đây sai ?
Cho các số tự nhiên n, k thỏa mãn $0 \le k < n.$ Trong các đẳng thức sau, đẳng thức nào đúng?

.png)
.png)
