Đề thi thử giữa học kỳ 2 môn Toán lớp 11 online - Mã đề 08
Vui lòng cài đặt đề thi trước khi làm bài
Giá trị của $\lim \frac{\cos n+\sin n}{n^{2}+1}$ bằng:
Giá trị của $\lim \frac{2}{n+1}$ bằng:
Giá trị của $\lim \frac{1-n^{2}}{n}$ bằng:
Giá trị của $\lim (2 n+1)$ bằng:
Tìm giới hạn $C=\lim\limits _{x \rightarrow+\infty}\left(\sqrt{4 x^{2}+x+1}-2 x\right)$
Tìm giới hạn $A=\lim\limits _{x \rightarrow+\infty}\left(\sqrt{x^{2}+x+1}-\sqrt[3]{2 x^{3}+x-1}\right)$
Tìm giới hạn $D=\lim\limits _{x \rightarrow-\infty} \frac{\sqrt[3]{1+x^{4}+x^{6}}}{\sqrt{1+x^{3}+x^{4}}}$
Tìm giới hạn $C=\lim\limits _{x \rightarrow+\infty} \frac{2 x+\sqrt{3 x^{2}+2}}{5 x-\sqrt{x^{2}+1}}$
$\text { Tính giới hạn } L=\lim \frac{\sqrt[3]{n}+1}{\sqrt[3]{n+8}} \text { . }$
$\text { Tính giới hạn } L=\lim \frac{\left(n^{2}+2 n\right)\left(2 n^{3}+1\right)(4 n+5)}{\left(n^{4}-3 n-1\right)\left(3 n^{2}-7\right)} \text { . }$
$\text { Tính giới hạn } L=\lim \frac{\left(2 n-n^{3}\right)\left(3 n^{2}+1\right)}{(2 n-1)\left(n^{4}-7\right)}$
Tìm tất cả các giá trị của tham số a để $L=\lim \frac{5 n^{2}-3 a n^{4}}{(1-a) n^{4}+2 n+1}>0$
Giả sử $\frac{{\sin \alpha }}{6}$, $\cos \alpha $, $\tan \alpha $ theo thứ tự đó là một cấp số nhân. Tính $\cos 2\alpha $.
:
Cho hình vuông (C1) có cạnh bằng a. Người ta chia mỗi cạnh của hình vuông thành bốn phần bằng nhau và nối các điểm chia một cách thích hợp để có hình vuông (C2) (Hình vẽ).
.png)
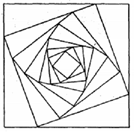
Từ hình vuông (C2) lại tiếp tục làm như trên ta nhận được dãy các hình vuông C1, C2, C3,.,Cn ... Gọi Si là diện tích của hình vuông ${C_i}\,\left( {i \in \left\{ {1,2,3,.....} \right\}} \right)$. Đặt $T = {S_1} + {S_2} + {S_3} + ...{S_n} + ...$. Biết $T = \frac{{32}}{3}$, tính a?
Cho dãy số (un) xác định bởi ${u_1} = - \frac{{41}}{{20}}$ và ${u_{n + 1}} = 21{u_n} + 1$ với mọi $n \ge 1.$ Tìm số hạng thứ 2018 của dãy số đã cho.
Cho dãy số (an) xác định bởi ${a_1} = 2,{a_{n + 1}} = - 2{a_n},n \ge 1,n \in N,{a_{n + 1}} = - 2{a_n},n \ge 1,n \in N$. Tính tổng của 10 số hạng đầu tiên của dãy số.
Cho cấp số cộng (un) có tất cả các số hạng đều dương thoả mãn ${u_1} + {u_2} + ... + {u_{2018}} = 4\left( {{u_1} + {u_2} + ... + {u_{1009}}} \right)$. Giá trị nhỏ nhất của biểu thức $P = \log _3^2{u_2} + \log _3^2{u_5} + \log _3^2{u_{14}}$ bằng
Cho cấp số cộng (un) có các số hạng đều dương, số hạng đầu u1 = 1 và tổng của 100 số hạng đầu tiên bằng 14950. Tính giá trị của tổng $S = \frac{1}{{{u_2}\sqrt {{u_1}} + {u_1}\sqrt {{u_2}} }} + \frac{1}{{{u_3}\sqrt {{u_2}} + {u_2}\sqrt {{u_3}} }} + ... + \frac{1}{{{u_{2018}}\sqrt {{u_{2017}}} + {u_{2017}}\sqrt {{u_{2018}}} }}$
Một rạp hát có 30 dãy ghế, dãy đầu tiên có 25 ghế. Mỗi dãy sau có hơn dãy trước 3 ghế. Hỏi rạp hát có tất cả bao nhiêu ghế?
Một tam giác vuông có chu vi bằng 3 và độ dài các cạnh lập thành một cấp số cộng. Độ dài các cạnh của tam giác đó là:
Một du khách vào trường đua ngựa đặt cược, lần đầu đặt 20000 đồng, mỗi lần sau tiền đặt gấp đôi lần tiền đặt cọc trước. Người đó thua 9 lần liên tiếp và thắng ở lần thứ 10. Hỏi du khác trên thắng hay thua bao nhiêu?
Người ta thiết kế một cái tháp gồm 11 tầng. Diện tích bề mặt trên của mỗi tầng bằng nữa diện tích của mặt trên của tầng ngay bên dưới và diện tích mặt trên của tầng 1 bằng nửa diện tích của đế tháp (có diện tích là 12288 m2). Tính diện tích mặt trên cùng.
Chu kì bán rã của nguyên tố phóng xạ poloni 210 là 138 ngày (nghĩa là sau 138 ngày khối lượng của nguyên tố đó chỉ còn một nửa). Tính (chính xác đến hàng phần trăm) khối lượng còn lại của 20 gam poloni 210 sau 7314 ngày (khoảng 20 năm).
Trong phương pháp quy nạp toán học, nếu ta giả sử mệnh đề đúng với (n = k ) thì ta cần chứng minh mệnh đề đúng đến:
Cho hình lăng trụ ABCD.A'B'C'D'. Hình chiếu vuông góc của A' lên (ABC) trùng với trực tâm H của tam giác ABC. Khẳng định nào sau đây không đúng?
Cho hình lập phương ABCD.A'B'C'D' cạnh bằng a. Khẳng định nào sau đây sai?
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Khẳng định nào sau đây sai?
Cho hình lập phương $ABCD.{A_1}{B_1}{C_1}{D_1}$. Mặt phẳng $\left( {{A_1}BD} \right)$ không vuông góc với mặt phẳng nào dưới đây?
Tìm mệnh đề đúng trong các mệnh đề sau:
Trong các mệnh đề sau, mệnh đề nào sai?
Trong không gian tập hợp các điểm M cách đều hai điểm cố định C và D là?
Mệnh đề nào sau đây có thể sai?
Cho hình lập phương $ABCD.{A_1}{B_1}{C_1}{D_1}$. Góc giữa AC và $D{A_1}$ là
Cho tứ diện ABCD có AB = AC = AD và $\widehat {BAC} = \widehat {BAD} = {60^0}$. Hãy xác định góc giữa cặp vectơ $\overrightarrow {AB} $ và $\overrightarrow {CD} $?
Cho hình lập phương ABCD.EFGH. Hãy xác định góc giữa cặp vectơ $\overrightarrow {AF} $ và $\overrightarrow {EG} $?
Cho $\overrightarrow a = 3{,^{}}\overrightarrow b = 5$ góc giữa $\vec a$ và $\vec b$ bằng 120o. Chọn khẳng định sai trong các khẳng định sau?
Cho hình lăng trụ $A B C \cdot A^{\prime} B^{\prime} C^{\prime}$, M là trung điểm của BB' . Đặt $\overrightarrow{C A}=\vec{a}, \overrightarrow{C B}=\vec{b}, \overrightarrow{A A^{\prime}}=\vec{c}$. Khẳng định nào sau đây đúng?
Cho ba vectơ$\vec{a}, \vec{b}, \vec{c}$ không đồng phẳng. Trong các khẳng định sau, khẳng định nào sai?
Cho hình hộp $A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ với tâm O . Hãy chỉ ra đẳng thức sai trong các đẳng thức sau đây:
Cho hình lập phương $A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ có cạnh bằng a . Hãy tìm mệnh đề sai trong những mệnh đề sau đây:

.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
