Trang chủ
lop-11
toan
Đề thi thử giữa học kỳ 2 môn Toán lớp 11 online - Mã đề 01

Đề thi thử giữa học kỳ 2 môn Toán lớp 11 online - Mã đề 01

Cài đặt đề thi

Thời gian làm bài

Không tính giờ

Tính giờ

phút

Chưa xem
Đã trả lời

Bạn có thể thử làm lại bài thi lần nữa

Trả lời đúng
Trả lời sai

Câu đúng

Câu sai

Điểm của bạn là

Làm lại lần nữa

Làm đề khác

Danh sách câu hỏi

Bấm vào ô số để xem câu hỏi

Vui lòng cài đặt đề thi trước khi làm bài

Câu 1

Nếu limu_n=L,u_n+9>0 ∀n thì $\lim\sqrt{u_n+9}$ bằng số nào sau đây?

A. L+9

B. L+3

C. $\sqrt{L+9}$

D. $\sqrt{L+3}$

Lời giải :

Vì limu_n = L nên lim⁡(u_n + 9) = L + 9 do đó lim$\sqrt{(u_n+9)}$=$\sqrt{(L+9)}$.

Chọn đáp án C

Câu 2

Tìm giới hạn sau: $\underset{x\to -1}{\mathop{\lim }}\,\left( -5{{x}^{2}}+7x-4 \right)$

A. 2

B. -5

C. -16

D. 16

Lời giải :

Ta có $\underset{x\to -1}{\mathop{\lim }}\,\left( -5{{x}^{2}}+7x-4 \right)$= -16

Câu 3

Tìm giới hạn sau $\underset{x\to 3}{\mathop{\lim }}\,\frac{9-{{x}^{2}}}{\sqrt{x+6}-3}$

A. -3

B. 34.

C. 12.

D. -36.

Lời giải :

$\mathop {\lim }\limits_{x \to 3} \frac{{9 - {x^2}}}{{\sqrt {x + 6} - 3}} = \mathop {\lim }\limits_{x \to 3} \frac{{(3 - x)(3 + x)\left( {\sqrt {x + 6} + 3} \right)}}{{x - 3}}$

$\mathop {\lim }\limits_{x \to 3} \left[ {( - 3 - x)\left( {\sqrt {x + 6} + 3} \right)} \right]\,\, = \,\, - 6.6\,\, = \,\, - 36$.

Câu 4

Tìm giới hạn sau: $\underset{x\to +\infty }{\mathop{\lim }}\,\left( \sqrt{{{x}^{2}}+x}-x \right)$

A. $ \frac{5}{2}$

B. $ -\frac{1}{2}$

C. $ \frac{1}{5}$

D. $ \frac{1}{2}$

Lời giải :

Ta có $\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {{x^2} + x} - x} \right)$=$\mathop {\lim }\limits_{x \to + \infty } \frac{{{x^2} + x - {x^2}}}{{\sqrt {{x^2} + x} + x}} = \frac{1}{2}$

Câu 5

Cho hàm số: $f(x)=\left\{ \begin{align} & \frac{\sqrt{7x-10}-2}{x-2},x>2 \\ & mx+3,x\le 2 \\\end{align} \right.$ . Tìm m để hàm số liên tục tại x = 2.

A. $m=3$

B. $m=-4$

C. $m=-\frac{5}{8}$

D. $m=-\frac{3}{2}$

Lời giải :

Ta có

$f(2) = \underset{x\to {{2}^{-}}}{\mathop{\lim f(x)}}\,=2m+3$
$\underset{x\to {{2}^{+}}}{\mathop{\lim }}\,f(x)\\ =\underset{x\to {{2}^{+}}}{\mathop{\lim }}\,\frac{7(x-2)}{(x-2)(\sqrt{7x-10}+2)}=\frac{7}{4}$

Do đó: $ 2m +3 = \frac{7}{4}$ $\Rightarrow m=-\frac{5}{8}$

Vậy $m=-\frac{5}{8}$ hàm số $f(x)$ liên tục tại x₀ = 2

Câu 6

Cho phương trình: $\left( {{m}^{4}}+m+1 \right){{x}^{2019}}+{{x}^{5}}-32\,\,=\,\,0$ , m là tham số. Khẳng định nào sau đây sai?

A. Phương trình trên vô nghiệm với mọi giá trị của tham số m.

B. Phương trình trên luôn có ít nhất một nghiệm trên (0;2) với mọi giá trị của tham số m.

C. Phương trình trên luôn có ít nhất một nghiệm dương trên (0;2) với mọi giá trị của tham số m.

D. Phương trình trên luôn có ít nhất một nghiệm dương với mọi giá trị của tham số m.

Lời giải :

Hàm số $f(x)=({{m}^{4}}+m+1){{x}^{2019}}+{{x}^{5}}-32$ là hàm đa thức nên liên tục trên $\mathbb{R}$ do đó nó liên tục trên đoạn [0; 2]

Ta có: $f(0)\,\,=\,\,-32$

+ $f(2)\,\,=\,\,\left( {{m}^{4}}+m+1 \right){{2}^{2019}}$

$={{2}^{2019}}\left[ {{\left( {{m}^{2}}-\frac{1}{2} \right)}^{2}}+{{\left( m+\frac{1}{2} \right)}^{2}}+\frac{1}{2} \right]\,\,>0$ $\forall m\in \mathbb{R}$.

Suy ra

$f(0).f(2)\,\,<\,\,0\,\,\,\forall m\in \mathbb{R}$

Nên phương trình f(x) = 0 có một nghiệm thuộc (0;2) nên có ít nhất một nghiệm với mọi giá trị của m.

Câu 7

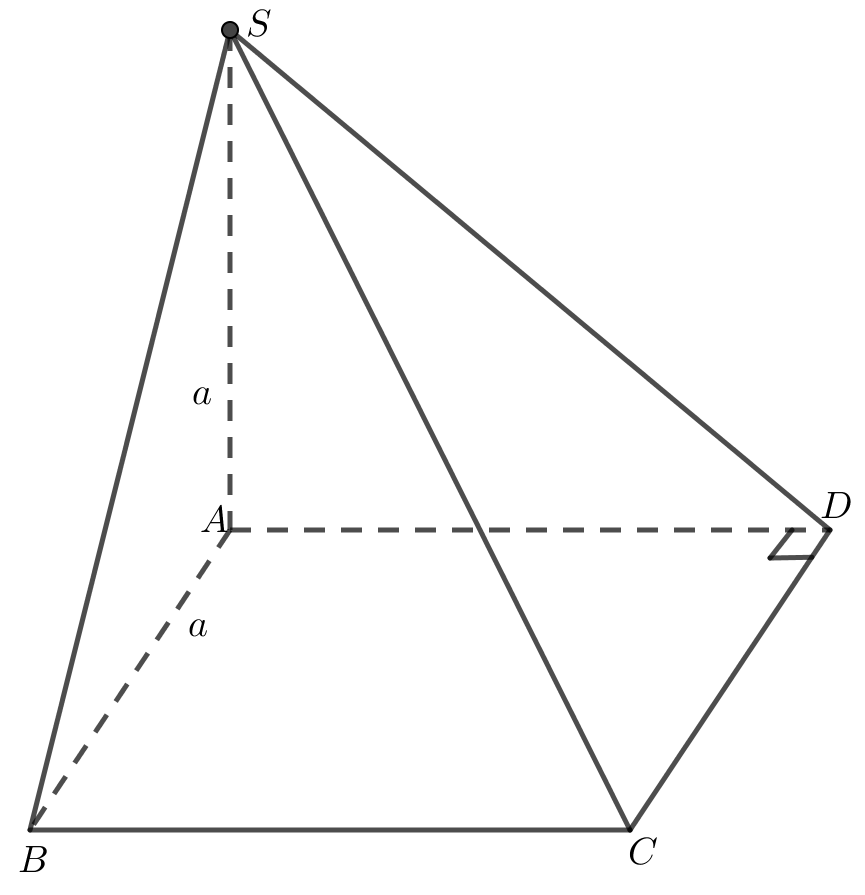
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, AB=BC= a, AD=2a; Cạnh bên SA vuông góc với mặt đáy và SA=a. Khẳng định nào sau đây là đúng?

A. BC vuông góc với mặt phẳng (SAB).

B. BC vuông góc với mặt phẳng (SAC).

C. BC vuông góc với mặt phẳng (SAD).

D. BC vuông góc với mặt phẳng (SBD).

Lời giải :

Ta có SA $\bot $(ABCD) nên SA $\bot $ BC

và AB $\bot $BC ( gt).

Suy ra BC $\bot $(SAB)

Mà SB $\subset $ (SAB) .Vậy tam giác SBC vuông tại B.

Chọn A.

Câu 8

Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, AB=BC= a, AD=2a; Cạnh bên SA vuông góc với mặt đáy và SA=a. Xác định và tính góc giữa SC và mặt phẳng (SAD).

A. ${25}^{0}$

B. ${80}^{0}$

C. ${42}^{0}$

D. ${35}^{0}$

Lời giải :

Dễ thấy tứ giác ABCI là hình vuông cạnh a .Ta có CI $\bot $AD và CI$\bot $SA, nên CI$\bot $(SAD),

SI là hình chiếu của SC trên (SAD), góc (SC, SAD) = góc CSI

Tam giác SCI vuông tại I ta có $tan\widehat{CSI}=\frac{CI}{SI}=\frac{a}{a\sqrt{2}}=\frac{\sqrt{2}}{2},CSI\approx {{35}^{0}}{{15}^{/}}$^.

Câu 9

Cho tứ diện ABCD có AB, AC, AD đôi một vuông góc với nhau. Gọi H là chân đường cao vẽ từ A của tam giác ACD. Khẳng dịnh nào sau đây đúng?

A. AC $\bot$ AH

B. BD $\bot$ CH

C. AB $\bot$ BH

D. CD $\bot$ BH

Lời giải :

Ta có AB $\bot$ AC, AB $\bot$ AD $\Leftrightarrow$ AB $\bot$ (ACD)

$\Leftrightarrow$ AB $\bot$ CD (1)

AH $\bot$ CD (2).

Từ (1) và (2) $\Leftrightarrow$ CD $\bot$ (AHB) $\Leftrightarrow$ CD $\bot$ BH

Câu 10

Cho tứ diện ABCD có AB, AC, AD đôi một vuông góc với nhau. Gọi H là chân đường cao vẽ từ A của tam giác ACD. Gọi K là chân đường cao vẽ từ A của tam giác ABH. Khẳng định nào sau đây đúng?

A. CK $\bot$ (ABD)

B. AH $\bot$ (BCD)

C. AK $\bot$ (BCD)

D. BH $\bot$ (ACD)

Lời giải :

Ta có AK $\bot$ BH, AK $\bot$ CD (do CD $\bot$ (AHB) (câu trên)

$\Leftrightarrow$ AK $\bot$ (BCD)

Câu 11

Tìm giới hạn sau: $\underset{x\to 1}{\mathop{\lim }}\,\frac{3{{\text{x}}^{2}}-2\text{x}-1}{{{x}^{3}}-1}$

A. $-\frac{4}{3}$

B. $-\frac{2}{5}$

C. $\frac{4}{3}$

D. $\frac{5}{9}$

Lời giải :

$\underset{x\to 1}{\mathop{\lim }}\,\frac{3{{\text{x}}^{2}}-2\text{x}-1}{{{x}^{3}}-1}=\underset{x\to 1}{\mathop{\lim }}\,\frac{(x-1)(3x+1)}{(x-1)({{x}^{2}}+x+1)}$.

$=\underset{x\to 1}{\mathop{\lim }}\,\frac{3x+1}{{{x}^{2}}+x+1}=\frac{4}{3}$.

Câu 12

Tìm giới hạn sau: $\underset{x\to {{3}^{-}}}{\mathop{\lim }}\,\frac{x+3}{x-3}$

A. $-1$

B. $1$

C. $+ \infty$

D. $- \infty$

Lời giải :

$\left\{ \begin{align} & \underset{x\to {{3}^{-}}}{\mathop{\lim }}\,(x-3)=0 \\ & x\to {{3}^{-}}\Leftrightarrow x-3<0 \\ & \underset{x\to {{3}^{-}}}{\mathop{\lim }}\,(x+3)=6>0 \\ \end{align} \right.$

Suy ra $\mathop {\lim }\limits_{x \to {3^ - }} \frac{{x + 3}}{{x - 3}} = - \infty$

Câu 13

Cho hàm số $f(x)=\left\{ \begin{align} & \frac{2{{\text{x}}^{2}}-3\text{x}-2}{2\text{x}-4}&khi\,\,x\ne 2 \\ & \frac{3}{2}&khi\,\,x=2 \\ \end{align} \right.$. Khẳng định nào sau đây là đúng?

A. Hàm số liên tục tại x = 2.

B. Hàm số không liên tục tại x = 2.

C. Hàm số liên tục trên R.

D. Hàm số không liên tục tại x = 1.

Lời giải :

$f(x)=\left\{ \begin{align} & \frac{2{{\text{x}}^{2}}-3\text{x}-2}{2\text{x}-4}&khi\,\,x\ne 2 \\ & \frac{3}{2}&khi\,\,x=2 \\\end{align} \right.$

Tập xác định D = R.

Tính được f(2) = $\frac{3}{2}$

$\underset{x\to 2}{\mathop{\lim }}\,f(x)=\underset{x\to 2}{\mathop{\lim }}\,\frac{2{{x}^{2}}-3x-2}{2x-4}$ $=\underset{x\to 2}{\mathop{\lim }}\,\frac{(x-2)(2x+1)}{2(x-2)}$ $=\underset{x\to 2}{\mathop{\lim }}\,\frac{2x+1}{2}=\frac{5}{2}$

Kết luận hàm số không liên tục tại x = 2.

Câu 14

Tìm giới hạn sau: $\lim \left( {\sqrt {9{n^2} + 2n - 1} - 3n} \right).$

A. $-\frac{1}{3}$

B. $\frac{-2}{3}$

C. $\frac{1}{3}$

D. $\frac{2}{3}$

Lời giải :

$\begin{array}{l}\lim \left( {\sqrt {9{n^2} + 2n - 1} - 3n} \right)\\ = \lim \frac{{2n - 1}}{{\sqrt {9{n^2} + 2n - 1} + 3n}}\\ = \lim \frac{{2 - \frac{1}{n}}}{{\sqrt {9 + \frac{2}{n} - \frac{1}{{{n^2}}}} + 3}} = \frac{1}{3}\end{array}$

Câu 15

Mệnh đề nào đúng trong các mệnh đề sau?

A. Góc giữa hai đường thẳng bằng góc giữa hai vectơ chỉ phương của hai đường thẳng đó.

B. Góc giữa hai đường thẳng là góc nhọn.

C. Góc giữa hai đường thẳng $a$ và $b$ bằng góc giữa hai đường thẳng $a$ và $c$ khi $b$ song song với $c$ (hoặc $b$ trùng với $c$).

D. Góc giữa hai đường thẳng $a$ và $b$ bằng góc giữa hai đường thẳng $a$ và $c$ thì $b$ song song với $c$.

Lời giải :

Đáp án C.

+) Đáp án A sai vì góc giữa hai đường thẳng có thể bằng hoặc bù với góc giữa hai véc tơ chỉ phương.

+) Đáp án B sai vì có thể là góc ${{90}^{0}}$.

Câu 16

Mệnh đề nào đúng trong các mệnh đề sau?

A. Góc giữa đường thẳng và mặt phẳng bằng góc giữa đường thẳng đó và hình chiếu của nó trên mặt phẳng đã cho.

B. Góc giữa đường thẳng $a$ và mặt phẳng $\left( P \right)$ bằng góc giữa đường thẳng $b$ và mặt phẳng $\left( P \right)$ khi $a$ và $b$ song song (hoặc $a$ trùng với $b$).

C. Góc giữa đường thẳng $a$ và mặt phẳng $\left( P \right)$ bằng góc giữa đường thẳng $a$ và mặt phẳng $\left( Q \right)$ thì mặt phẳng $\left( P \right)$ song song với mặt phẳng $\left( Q \right)$.

D. Góc giữa đường thẳng $a$ và mặt phẳng $\left( P \right)$ bằng góc giữa đường thẳng $b$ và mặt phẳng $\left( P \right)$ thì $a$ và $b$ song song.

Lời giải :

Đáp án B.

+) Đáp án A sai vì khi đường thẳng đó vg với mặt phẳng.

+) Đáp án C, D: Vẽ hình thấy có vô số đường thẳng và mặt phẳng thỏa mãn.

Câu 17

Mệnh đề nào đúng trong các mệnh đề sau?

A. Góc giữa hai mặt phẳng luôn là góc nhọn.

B. Góc giữa mặt phẳng $\left( P \right)$ và mặt phẳng $\left( Q \right)$bằng góc giữa mặt phẳng $\left( P \right)$ và mặt phẳng $\left( R \right)$ khi mặt phẳng $\left( R \right)$ song song với mặt phẳng $\left( Q \right)$ (hoặc $\left( R \right)$ trùng với $\left( Q \right)$).

C. Góc giữa mặt phẳng $\left( P \right)$ và mặt phẳng $\left( Q \right)$bằng góc giữa mặt phẳng $\left( P \right)$ và mặt phẳng $\left( R \right)$ thì mặt phẳng $\left( R \right)$ song song với mặt phẳng $\left( Q \right)$.

D. Cả ba mệnh đề trên đều đúng.

Lời giải :

Đáp án B.

+) Đáp án A sai vì vì có thể là vg.

+) Đáp án C sai vì chẳng hạn $\left( Q \right)$ và $\left( R \right)$ cắt nhau, $\left( P \right)$ là mặt phẳng phân giác.

Câu 18

Cho hình chóp $S.ABCD$ có đáy là hình vuông cạnh $a$, đường thẳng $SA$ vuông góc với mặt phẳng đáy, $SA=a$. Góc giữa mặt phẳng $\left( SCD \right)$ và mặt phẳng $\left( ABCD \right)$ là $\alpha $. Khi đó $\tan \alpha $ nhận giá trị nào trong các giá trị sau:

A. $\tan \alpha =\frac{\sqrt{2}}{2}$.

B. $\tan \alpha =1$

C. $\tan \alpha =\sqrt{2}$.

D. $\tan \alpha =\sqrt{3}$.

Lời giải :

Đáp án B.

Ta có: $\left\{ \begin{align} & CD\bot AD \\ & CD\bot SA \\\end{align} \right.$$\Rightarrow CD\bot \left( SAD \right)\Rightarrow \alpha =\widehat{SDA}$.

Mà $\vartriangle SDA$ vuông cân tại $A$ nên $\widehat{SDA}={{45}^{0}}$ .

Câu 19

Cho hình lập phương $ABCD.{A}'{B}'{C}'{D}'$. Xét mặt phẳng $\left( {A}'BD \right)$, trong các mệnh đề sau, mệnh đề nào đúng?

A. Góc giữa mặt phẳng $\left( {A}'BD \right)$ và các mặt phẳng chứa các mặt của hình lập phương bằng nhau.

B. Góc giữa mặt phẳng $\left( {A}'BD \right)$ và các mặt phẳng chứa các mặt của hình lập phương bằng nhau.

C. Góc giữa mặt phẳng $\left( {A}'BD \right)$ và các mặt phẳng chứa các mặt của hình lập phương bằng $\alpha $ mà $\tan \alpha =\frac{1}{\sqrt{2}}$.

D. Cả ba mệnh đề trên đều sai.

Lời giải :

Đáp án A.

Đáp án B, C vì giả sử ta xác định góc giữa $\left( A'BD \right)$ và $\left( ABCD \right)$ là góc $\widehat{A'IA}$ với $I$ là trung điểm của $BD$

và $\cos \widehat{AIA'}=\frac{A{{I}^{2}}+A'{{I}^{2}}-AA{{'}^{2}}}{2.AI.A'I}$

$=\frac{{{\left( \frac{a\sqrt{2}}{2} \right)}^{2}}+{{\left( \frac{a\sqrt{6}}{2} \right)}^{2}}-{{a}^{2}}}{2.\frac{a\sqrt{2}}{2}.\frac{a\sqrt{6}}{2}}$

$=\frac{\frac{2{{a}^{2}}}{4}+\frac{6{{a}^{2}}}{4}-{{a}^{2}}}{\frac{2{{a}^{2}}\sqrt{12}}{4}}$

$=\frac{4{{a}^{2}}}{2{{a}^{2}}12}=\frac{1}{\sqrt{3}}$

$\Rightarrow \cos \alpha =\frac{1}{\sqrt{3}}\Rightarrow \tan \alpha \ne \frac{1}{\sqrt{2}}$

Câu 20

Cho hình chóp tứ giác $S.ABCD$ có đáy là hình vuông và có một mặt bên vuông góc với đáy. Xét bốn mặt phẳng chứa bốn mặt bên và mặt phẳng chứa mặt đáy. Trong các mệnh đề sau, mệnh đề nào đúng?

A. Có hai cặp mặt phẳng vuông góc nhau.

B. Có ba cặp mặt phẳng vuông góc nhau.

C. Có bốn cặp mặt phẳng vuông góc nhau.

D. Có năm cặp mặt phẳng vuông góc nhau.

Lời giải :

Đáp án B.

Giả sử hình chóp đó là $S.ABCD$. Ta có $\left( SAB \right)\bot \left( ABCD \right);\left( SAB \right)\bot \left( SAD \right);\left( SAD \right)\bot \left( ABCD \right)$

Câu 21

Cho hình lập phương $ABCD.EFGH$, hãy xác định góc giữa cặp vectơ $\overrightarrow{AB},\ \overrightarrow{DH}$?

A. ${{45}^{0}}$.

B. ${{90}^{0}}$.

C. ${{120}^{0}}$.

D. ${{60}^{0}}$.

Lời giải :

Đáp án B.

$\left( \overrightarrow{AB};\overrightarrow{DH} \right)=\left( \overrightarrow{DC};\overrightarrow{DH} \right)={{90}^{0}}$.

Câu 22

Trong không gian cho ba đường thẳng phân biệt $a,\ b,\ c$. Mệnh đề nào sau đây đúng?

A. Nếu $a$ và $b$ cùng vuông góc với $c$ thì $a//b$.

B. Nếu $a//b$, $c\bot a$ thì $c\bot b$.

C. Nếu góc giữa $a$ và $c$ bằng góc giữa $b$ và $c$ thì $a//b$.

D. Nếu $a$ và $b$ cùng nằm trong mặt phẳng $\left( \alpha \right)$ và $c//\left( \alpha \right)$ thì góc giữa $a$ và $c$ bằng góc giữa $b$ và $c$.

Lời giải :

Đáp án B.

Câu 23

Cho hình chóp $S.ABC$ có $SA=SB=SC,\ \widehat{ASB}=\widehat{BSC}=\widehat{CSA}$. Hãy xác định góc giữa $SB$ và $AC$.

A. ${{60}^{0}}$.

B. ${{120}^{0}}$

C. ${{45}^{0}}$.

D. ${{90}^{0}}$.

Lời giải :

Đáp án D.

Từ giả thiết suy ra các mặt của hình chóp đều là các tam giác đều. Gọi $M,N,P$ lần lượt là trung điểm của $SA,SC,BC$. Giả sử cạnh hình chóp đều là \[\text{a}\]thì $MN=NP=\frac{a}{2};MP\bot SA$vì $\vartriangle SAP$ cân tại $P$.

$PM=\sqrt{{{\left( \frac{a\sqrt{3}}{2} \right)}^{2}}-{{\left( \frac{a}{2} \right)}^{2}}}=\sqrt{\frac{3{{a}^{2}}}{4}-\frac{{{a}^{2}}}{4}}=\frac{a\sqrt{2}}{2};\cos \widehat{MNP}=\frac{M{{N}^{2}}+N{{P}^{2}}-M{{P}^{2}}}{2.MN.NP}=\frac{\frac{{{a}^{2}}}{4}+\frac{{{a}^{2}}}{4}-\frac{2{{a}^{2}}}{4}}{2.\frac{a}{2}.\frac{a}{2}}$

$\cos \widehat{MNP}=0\Rightarrow \widehat{\left( SB,AC \right)}={{90}^{0}}$.

Cách 2: Lấy $I$ là trung điểm của $AC$ta có: $AC\bot \left( SIB \right)\Rightarrow AC\bot SB$.

Cách 3: $\overrightarrow{SB}.\overrightarrow{AC}=\overrightarrow{SB}\left( \overrightarrow{SC}-\overrightarrow{SA} \right)=\overrightarrow{SB}.\overrightarrow{SC}-\overrightarrow{SB}.\overrightarrow{SA}=0$.

Câu 24

Cho tứ diện $ABCD$ có hai mặt $ABC,\ ABD$ là các tam giác đều. Góc giữa $AB$ và $CD$ là

A. ${{120}^{0}}$.

B. ${{60}^{0}}$.

C. ${{90}^{0}}$.

D. ${{30}^{0}}$.

Lời giải :

Đáp án C.

Gọi $I$ là trung điểm của $AB\Rightarrow AB\bot (IDC)\Rightarrow AB\bot CD$.

Ngoài ra ta cũng có thể sử dụng tích vô hướng để giải quyết bài toán này.

Câu 25

Cho hình hộp $ABCD.{A}'{B}'C{D}'$. Giả sử tam giác $A{B}'C,\ {A}'D{C}'$ là các tam giác nhọn. Góc giữa hai đường thẳng $AC$ và ${A}'D$ là góc nào sau đây?

A. $\widehat{A{B}'C}$.

B. $\widehat{D{A}'C}$.

C. $\widehat{B{B}'C}$.

D. $\widehat{DAC}$.

Lời giải :

Đáp án B.

Ta có: $AC//A'C'\Rightarrow \widehat{\left( AC,A'D \right)}=\widehat{\left( A'C',A'D \right)}=\widehat{DA'C'}$ (góc nhọn).

Câu 26

Trong các mệnh đề sau, mệnh đề nào đúng?

A. Cho hai đường thẳng song song, đường thẳng nào vuông góc với đường thẳng thứ nhất thì cũng vuông góc với đường thẳng thứ hai.

B. Trong không gian, hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì song song với nhau.

C. Hai đường thẳng phân biệt vuông góc với nhau thì chúng cắt nhau.

D. Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì vuông góc với nhau.

Lời giải :

Đáp án A.

Câu 27

Cho tứ diện $ABCD$. Gọi $I$, $J$, $K$ lần lượt là trung điểm của $BC$, $CA$ và $BD$. Khi đó góc giữa $AB$ và $CD$ là:

A. $\widehat{JIK}$.

B. $\widehat{ABC}$.

C. $\widehat{IJK}$.

D. $\widehat{JKI}$.

Lời giải :

Đáp án A.

Câu 28

Cho một hình thoi $ABCD$ cạnh $a$ và một điểm $S$ nằm ngoài mặt phẳng chứa hình thoi sao cho $SA=a$ và vuông góc với $\left( ABC \right)$. Tính góc giữa $SD$ và $BC$

A. ${{60}^{\circ }}$.

B. ${{90}^{\circ }}$.

C. ${{45}^{\circ }}$.

D. $\arctan \sqrt{2}$.

Lời giải :

Đáp án C.

Ta có: $AD//BC\Rightarrow \widehat{\left( SD,BC \right)}=\widehat{\left( SD,AD \right)}=\widehat{ADS}={{45}^{0}}$.

Câu 29

Cho tứ diện $ABCD$.Gọi $M$, $N$, $I$ lần lượt là trung điểm của $BC$, $AD$ và $AC$. Cho $AB=2a$ , $CD=2a\sqrt{2}$ và $MN=a\sqrt{5}$. Tính góc $\varphi =\left( \widehat{AB,CD} \right)$

A. ${{135}^{\circ }}$.

B. ${{60}^{\circ }}$.

C. ${{90}^{\circ }}$.

D. ${{45}^{\circ }}$.

Lời giải :

Đáp án D.

Theo tính chất đường trung bình trong tam giác:

$\left\{ \begin{align}& IN//CD;IN=\frac{1}{2}CD=a\sqrt{2} \\& IM//AB;IM=\frac{1}{2}AB=a \\\end{align} \right.$

$\Rightarrow \varphi =\widehat{\left( AB,CD \right)}=\widehat{\left( IM,IN \right)}$. Áp dụng định lý cosin ta có:

$\cos \varphi =\left| \frac{I{{M}^{2}}+I{{N}^{2}}-M{{N}^{2}}}{2.IM.IN} \right|=\left| -\frac{\sqrt{2}}{2} \right|=\frac{\sqrt{2}}{2}\Rightarrow \varphi ={{45}^{0}}$.

Câu 30

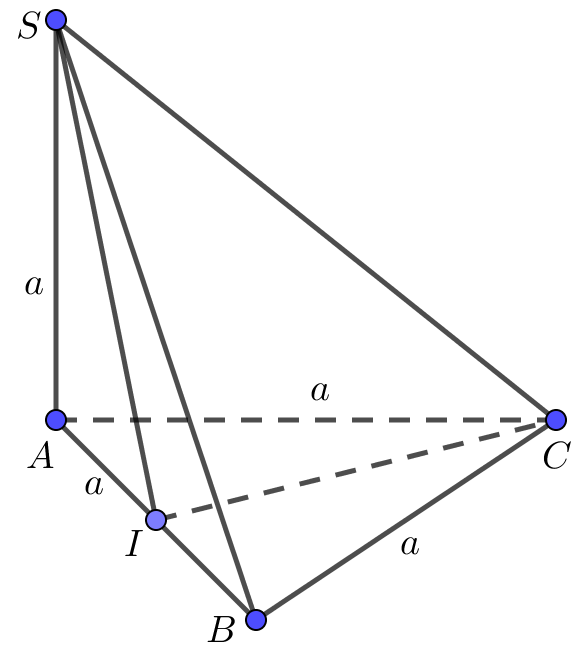
Cho hình chóp $S.ABC$ có $SA\bot \left( ABC \right)$, $SA=a$, $\Delta ABC$ đều cạnh $a$. Tính góc giữa $SB$ và $\left( ABC \right)$.

A. $\arctan 2$.

B. ${{60}^{\circ }}$.

C. ${{45}^{\circ }}$.

D. ${{90}^{\circ }}$.

Lời giải :

Đáp án C.

Ta có $SA\bot \left( ABC \right)\Rightarrow AB$ là hình chiếu của $SB$trên mặt phẳng $\left( ABC \right)\Rightarrow \varphi =\widehat{ASB}=\widehat{\left( SD,AD \right)}={{45}^{0}}$.

Kết quả

Nộp bài

Kết quả

Hoàn thành

Đề thi thử giữa học kỳ 2 môn Toán lớp 11 online - Mã đề 01

Trở thành Membership ngay

MEGA-AI phản hồi

Đăng nhập