Megaedu.AI - Thi thử trực tuyến , có chấm điểm và đáp án chi tiết.

Câu 1

Phương trình tổng quát của đường thẳng đi qua hai điểm A(3 ; -1) và B(1 ; 5) là:

A. -x + 3y + 6 = 0 ;

B. 3x - y + 10 = 0 ;

C. 3x - y + 6 = 0 ;

D. 3x + y - 8 = 0.

Câu 2

Phương trình đường thẳng cắt hai trục tọa độ tại A(-2 ; 0) và B(0 ; 3) là:

A. 2x - 3y + 4 = 0 ;

B. 3x - 2y + 6 = 0 ;

C. 3x - 2y - 6 = 0 ;

D. 2x - 3y - 4 = 0.

Lời giải :

Phương trình đường thẳng: $\frac{x}{- 2} + \frac{y}{3} = 1 \Leftrightarrow$ 3x - 2y + 6 = 0

Câu 3

Xét vị trí tương đối của hai đường thẳng:

d1: x – 2y + 1 = 0 và d2: – 3x + 6y – 10 = 0

A. Trùng nhau.

B. Song song.

C. Vuông góc với nhau.

D. Cắt nhau nhưng không vuông góc nhau.

Câu 4

Tọa độ tâm I và bán kính R của đường tròn $(C):(x−1)^2+(y+3)^2=16$ là:

A. I (-1; 3), R = 4;

B. I (1; -3), R = 4;

C. I (1; -3), R = 16

D. I (-1; 3), R = 16.

Câu 5

Đường tròn $(C): x^2 + y^2 – 6x + 2y + 6 = 0$ có tâm I và bán kính R lần lượt là:

A. I(3; −1) và R = 4;

B. I(3; 1) và R = 4;

C. I(3; −1) và R = 2;

D. I(-6; 2) và R = 2.

Câu 6

Cho parabol (P) có phương trình chính tắc là ${y^2} = 2px$, với p > 0. Khi đó khẳng định nào sau đây sai?

A. Tọa độ tiêu điểm F(p/2;0);

B. Phương trình đường chuẩn Δ:x+p/2=0;

C. Trục đối xứng của parabol là trục Oy.

D. Parabol nằm về bên phải trục Oy.

Câu 7

Biểu thức nào sau đây là tam thức bậc hai

A. $f(x) = x + 2$;

B. $f(x) = 2x ^3 + 2x2 – 1$;

C. $f(x) = x^2 – 3x$;

D. $f(x) = 2x – 1$.

Câu 8

Các giá trị m làm cho biểu thức $f(x) = x^2 + 4x + m + 3$ luôn dương là

A. m < 1;

B. m ≥ 1;

C. m > 1;

D. m∈∅.

Lời giải :

Đáp án đúng là: C

Ta có: f(x) = x²+ 4x + m + 3 luôn luôn dương x² + 4x + m + 3 > 0 với mọi x ℝ $\Leftrightarrow {\begin{cases} a = 1 > 0 \\ Δ^{'} = 2^{2} - (m + 3) < 0 \end{cases} \Leftrightarrow {\begin{cases} a = 1 > 0 \\ m > 1 \end{cases}$ .

Vậy đáp án đúng là C.

Câu 9

Tập nghiệm của bất phương trình $x^2$ – x – 6 ≤ 0 là:

A. (–∞; – 3]∪[2; + ∞);

B. [– 3; 2];

C. [– 2; 3];

D. (– ∞; – 2]∪[3; + ∞) ;

Câu 10

Phương trình:$\sqrt { - {x^2} + 6x - 5} = 8 - 2x$ có nghiệm là:

A. x = 3 ;

B. x = 23/5;

C. x = 3 hoặc x = 23/5 ;

D. x = – 3.

Lời giải :

Đáp án đúng là: A

Bình phương hai về ta có:

– x² + 6x – 5 = (8 – 2x)²

⇒ – x² + 6x – 5 = 4x² – 32x + 64

⇒ – 5x² + 38x – 69 = 0

⇒ x = 3 hoặc x = $\frac{23}{5}$

Thay lần lượt các nghiệm trên vào phương trình đã cho, ta thấy x = 3 thoả mãn

Vậy phương trình có nghiệm x = 3

Câu 11

Cho các chữ số 2, 3, 4, 5, 6, 7 số các số tự nhiên chẵn có 3 chữ số lập thành từ các chữ số đã cho là:

A. 36;

B. 18;

C. 256;

D. 108;

Lời giải :

Đáp án đúng là: D

Gọi số tự nhiên có 3 chữ số cần tìm là: $\overline {abc} $ $\bar{}$ (a ≠ 0; a, b, c ∈ {2; 3; 4; 5; 6; 7}) khi đó:

Công đoạn 1. Chọn chữ số c có 3 cách chọn ( vì $\overline {abc} $ là số chẵn nên c chỉ có thể chọn một trong các số 2, 4, 6).

Công đoạn 2. Chọn chữ số a có 6 cách chọn (vì a được chọn tuỳ ý nên a có thể chọn một trong 6 số 2, 3, 4, 5, 6, 7).

Công đoạn 3. Chọn số b có 6 cách chọn (vì b được chọn tuỳ ý nên b có thể chọn một trong 6 số 2, 3, 4, 5, 6, 7).

Vậy áp dụng quy tắc nhân, số các số tự nhiên chẵn có 3 chữ số là được lập từ các số trên là: 6.6.3 = 108 (số).

Câu 12

Bạn Dũng có 8 quyển truyện tranh khác nhau và 7 quyển tiểu thuyết khác nhau. Bạn Dũng có bao nhiêu cách chọn ra một quyển sách để đọc vào cuối tuần.

A. 8;

B. 7;

C. 56;

D. 15.

Câu 13

Tên 15 học sinh được ghi vào 15 tờ giấy để vào trong hộp. Có bao nhiêu cách chọn tên 4 học sinh để cho đi du lịch

A. 4!;

B. 15!.

C. 1365;

D. 32760.

Lời giải :

Đáp án đúng là: C

Mỗi cách chọn ra 4 học sinh trong 15 học sinh là một tổ hợp chập 4 của 15 phần tử. Vậy số cách chọn ra 4 học sinh là: $C_{15}^{4}$ = 1365 (cách).

Câu 14

Trong khai triển nhị thức $(a + 2)^{n + 6}$ (n ∈ ℕ). Có tất cả 17 số hạng. Vậy n bằng

A. 17;

B. 11;

C. 10;

D. 12.

Câu 15

Gieo một đồng tiền liên tiếp 3 lần thì số phần tử của không gian mẫu n(Ω) là

A. 4

B. 6

C. 8

D. 16

Câu 16

Gieo một con xúc xắc cân đối đồng chất 2 lần. Số phần tử của không gian mẫu là?

A. 6;

B. 12;

C. 18;

D. 36.

Câu 17

Cho A là một biến cố liên quan đến phép thử T. Mệnh đề nào sau đây là mệnh đề đúng?

A. P(A) là số lớn hơn 0;

B. P(A) = 1 – P($\overline A $);

C. P(A) = 0 ⇔ A = Ω;

D. P(A) là số nhỏ hơn 1.

Câu 18

Một lớp có 20 học sinh nam và 18 học sinh nữ. Chọn ngẫu nhiên một học sinh. Xác suất chọn được 1 học sinh nữ là:

A. 1/38

B. 10/19

C. 9/19

D. 19/9

Lời giải :

Đáp án đúng là: C

Ta có : Mỗi lần chọn 1 học sinh ngẫu nhiên từ 38 học sinh cho ta một tổ hợp chập 1 của 38 nên n(Ω) = $C_{38}^{1}$ = 38.

Gọi H là biến cố:”học sinh được chọn là học sinh nữ”.

⇒ n(H) = 18.

Vậy P(G) = $\frac{{n\left( H \right)}}{{n\left( \Omega \right)}}$ = $\frac{18}{38}$ = $\frac{9}{19}$ .

Câu 19

Phép thử ngẫu nhiên (gọi tắt là phép thử) là gì?

A. Hoạt động mà ta không thể biết trước được kết quả của nó;

B. Hoạt động mà ta có thể biết trước được kết quả của nó;

C. Hoạt động mà ta gieo xúc xắc;

D. Cả 3 phương án trên đều sai.

Câu 20

Trong các thí nghiệm sau thí nghiệm nào không phải là phép thử ngẫu nhiên:

A. Gieo đồng tiền xem xuất hiện mặt ngửa hay mặt sấp;

B. Gieo 3 đồng tiền và xem có mấy đồng tiền lật ngửa;

C. Chọn bất kì 1 học sinh trong lớp và xem là nam hay nữ;

D. Bỏ hai viên bi xanh và ba viên bi đỏ trong một chiếc hộp, sau đó lấy từng viên một để đếm xem có tất cả bao nhiêu viên bi.

Câu 21

Cho tam thức bậc hai f(x) = ax$^2$ + bx + c có đồ thị như hình vẽ dưới đây

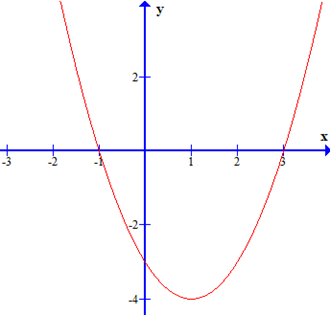
Bảng biến thiên của tam thức bậc hai là

A.

B.

C.

D.

Câu 22

Cho phương trình $x^2$ – 2x – m = 0. Tìm tất cả các giá trị của m để phương trình có 2 nghiệm thỏa mãn $x_1 < x_2 < 2$.

A. m > 0;

B. m > 0;

C. – 1 < m < 0;

D. m > 1.

Lời giải :

Đáp án đúng là: C

Phương trình có hai nghiệm phân biệt ∆’ > 0 $\Leftrightarrow$ $\Leftrightarrow$ (– 1)2 + m > 0 $\Leftrightarrow$ $\Leftrightarrow$ m > – 1.

Để phương trình có hai nghiệm thỏa mãn x1 < x2 < 2.

$\Leftrightarrow {\begin{cases} x_{1} - 2 + x_{2} - 2 < 0 \\ (x_{1} - 2) (x_{2} - 2) > 0 \end{cases}$ $\Leftrightarrow {\begin{cases} x_{1} + x_{2} - 4 < 0 \\ x_{1} x_{2} - 2 (x_{1} + x_{2}) + 4 > 0 \end{cases}$ $\Leftrightarrow {\begin{cases} 2 - 4 < 0 \\ - m - 2.2 + 4 > 0 \end{cases}$ ${\begin{cases} 2 - 4 < 0 \\ - m - 2.2 + 4 > 0 \end{cases}$

m < 0.

Kết hợp với điều kiện ta được: – 1 < m < 0.

Câu 23

Cho phương trình $\sqrt {{x^2} + 3} = \sqrt {2x + 6} $. Chọn khẳng định đúng:

A. Phương trình có hai nghiệm phân biệt cùng dấu;

B. Phương trình có hai nghiệm phân biệt trái dấu;

C. Phương trình có một nghiệm;

D. Phương trình vô nghiệm.

Lời giải :

Bình phương hai vế của phương trình đã cho, ta được:

x² + 3 = 2x + 6.

⇒ x² – 2x – 3 = 0

⇒ x = 3 hoặc x = –1.

Với x = 3, ta có $\sqrt{3^{2} + 3} = \sqrt{2.3 + 6}$ (đúng)

Với x = –1, ta có $\sqrt{{(- 1)}^{2} + 3} = \sqrt{2. (- 1) + 6}$ (đúng)

Vì vậy khi thay lần lượt các giá trị x = 3 và x = –1 vào phương trình đã cho, ta thấy x = 3 và x = –1 đều thỏa mãn.

Do đó nghiệm của phương trình đã cho là x = 3 > 0 hoặc x = –1 < 0.

Vậy phương trình đã cho có hai nghiệm trái dấu.

Ta chọn phương án B. Phương trình vô nghiệm.

Câu 24

Tập nghiệm của phương trình $\sqrt {\left( {x - 3} \right)\left( {2 - x} \right)} = \sqrt {4{x^2} + 12x + 9} $ là:

A. {10; 3};

B. {5};

C. {3};

D. ∅.

Lời giải :

Đáp án đúng là: D

$\sqrt{(x - 3) (2 - x)} = \sqrt{4 x^{2} + 12 x + 9}$

$\Leftrightarrow \sqrt{- x^{2} + 5 x - 6} = \sqrt{4 x^{2} + 12 x + 9}$

Bình phương hai vế phương trình trên, ta được:

–x² + 5x – 6 = 4x² + 12x + 9

⇒ 5x² + 7x + 15 = 0 (vô nghiệm)

Vậy tập nghiệm của phương trình đã cho là ∅.

Ta chọn phương án D.

Câu 25

Giả sử ta dùng 5 màu để tô cho 3 nước khác nhau trên bản đồ và không có màu nào được dùng hai lần. Số các cách để chọn những màu cần dùng là:

A. 60;

B. 8;

C. 15;

D. 53.

Lời giải :

Đáp án đúng là: A

Mỗi cách chọn lần lượt 3 trong 5 màu để tô 3 nước khác nhau là một chỉnh hợp chập 3 của 5 phần tử.

Vậy số cách chọn là $A_{5}^{3}$ = 60 (cách)

Câu 26

Có bao nhiêu cách xếp 5 người thành một hàng dọc

A. 120;

B. 5;

C. 20;

D. 25.

Câu 27

Chọn ngẫu nhiên một số nguyên dương không lớn hơn 15. Hãy mô ta không gian mẫu trên?

A. Ω = {1; 2; 3; 4; 5; 6; 7; 10; 11; 12; 13; 14; 15};

B. Ω = {1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13; 14};

C. Ω = {0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13; 14};

D. Ω = {1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13; 14; 15}.

Câu 28

Từ các chữ số 1; 2; 4; 6; 8; 9 lấy ngẫu nhiễn một số. Xác suất để lấy được một số nguyên tố là:

A. 1/2

B. 1/3

C. 1/4

D. 1/6

Lời giải :

Đáp án đúng là: D

Ta có : Mỗi lần chọn 1 số bất kì từ 6 số đã cho, ta được một tổ hợp chập 1 của 6 nên n(Ω) = $C_{6}^{1}$ = 6

Gọi B là biến cố :”Số lấy ra là số nguyên tố”

Ta có: B = {2} ⇒ n(B) = 1

Vậy P(B) =$\frac{{n\left( B \right)}}{{n\left( \Omega \right)}} = \frac{1}{6}$

Câu 29

Có 3 chiếc hộp, hộp A chứa 1 chiếc bút xanh, 1 chiếc bút đỏ; hộp B chứa 1 chiếc bút đỏ, 1 chiếc bút tím; hộp C chứa 1 chiếc bút đỏ, 1 chiếc bút tím. Lấy ngẫu nhiên từ mỗi hộp 1 chiếc bút. Ta có sơ đồ cây sau:

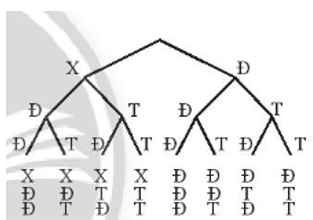
Dựa vào sơ đồ cây cho biết số kết quả thuận lợi cho biến cố H: “Trong 3 bút lấy ra có đúng 1 bút đỏ”.

A. 1

B. 2

C. 3

D. 8

Câu 30

Cho phương trình $x^2 + y^2$ – 2mx – 4(m – 2)y + 6 – m = 0. Điều kiện của m để phương trình đã cho là một phương trình đường tròn là:

A. m ∈ ℝ;

B. m∈(−∞;1)∪(2;+∞)

C. m∈(−∞;1]∪[2;+∞)

D. m∈(−∞;1/3)∪(2;+∞)

x	–∞ –2 3 + ∞
f(x)	+ 0 – 0 +

Đề thi thử học kỳ 2 môn Toán lớp 10 online - Mã đề 01

Trở thành Membership ngay

MEGA-AI phản hồi

Đăng nhập