Đề thi thử học kỳ 1 môn Toán lớp 10 online - Mã đề 07
Vui lòng cài đặt đề thi trước khi làm bài
Tập $S = \left\{ {\left. {q \in \mathbb{Q}} \right|25{q^4} - 9{q^2} = 0} \right\}$ có bao nhiêu phần tử?
Cho hàm số $y = f\left( x \right)$ có tập xác định là $\left[ { - 3;3} \right]$và đồ thị của nó được biểu diễn bởi hình bên.
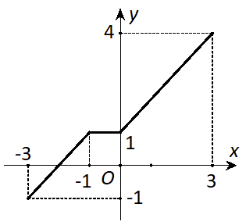
Khẳng định nào sau đây là đúng?
Tìm tập xác định D của hàm số $y = \frac{{3x - 1}}{{2x - 2}}$.
Hàm số $y = {\rm{ \;}} - {x^2} + 2x + 3$ có đồ thị là hình nào trong các hình sau?
Điểm nào sau đây thuộc đồ thị hàm số $y = \frac{1}{{x - 1}}$.
Bảng xét dấu nào sau đây là bảng xét dấu của tam thức $f\left( x \right) = {x^2} + 12x + 36$?
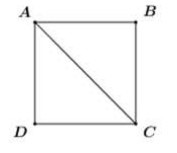
Cho tứ giác ABCD. Điều kiện nào là điều kiện cần và đủ để $\overrightarrow {AB} {\rm{ \;}} = \overrightarrow {CD} $?
Cho bốn điểm A, B, C, D phân biệt. Khi đó, $\overrightarrow {AB} {\rm{ \;}} - \overrightarrow {DC} {\rm{ \;}} + \overrightarrow {BC} {\rm{ \;}} - \overrightarrow {AD} $ bằng véctơ nào sau đây?
Gọi $M,{\mkern 1mu} {\mkern 1mu} N$ lần lượt là trung điểm của các cạnh $AB,{\mkern 1mu} {\mkern 1mu} AC$ của tam giác đều ABC. Hỏi đẳng thức nào dưới đây đúng?
Xác định hàm số bậc hai $y = a{x^2} - x + c$ biết đồ thị hàm số đi qua A(1;-2) và B(2;3).
Giá trị nhỏ nhất của hàm số $y = {x^2} - 4x + 5$ là:
Các giá trị $m$ làm cho biểu thức $f\left( x \right) = {x^2} + 4x + m - 5$ luôn luôn dương là
Tập xác định của hàm số $y = \sqrt {\frac{2}{{{x^2} + 5x - 6}}} $ là:
Giải phương trình: $\sqrt {{x^2} - 4x - 1} {\rm{\;}} = 2$.
Cho tam giác ABC đều cạnh bằng $1$, trọng tâm $G$. Độ dài vectơ $\overrightarrow {AG} $ bằng:
Cho ngũ giác ABCDE. Từ đỉnh của ngũ giác đã cho lập được bao nhiêu vecto (khác $\overrightarrow 0 $) có điểm cuối là điểm A?
Cho các vecto $\vec a$ và $\vec b$ thỏa mãn $\left| {\vec a} \right| = 2$, $\left| {\vec b} \right| = 1$ và $\left( {\vec a,{\mkern 1mu} {\mkern 1mu} \vec b} \right) = {60^0}$. Tính góc giữa vecto $\vec a$ và vecto $\vec c = \vec a - \vec b$.
Cho tam giác ABC vuông tại A có AB = 3, BC = 5. Tính $\left| {\overrightarrow {AB} {\rm{ \;}} - \overrightarrow {CB} } \right|$
Cho hình bình hành ABCD có $M$ là trung điểm của AC. Phân tích vectơ $\overrightarrow {DM} $ theo hai vectơ $\overrightarrow {BC} $ và $\overrightarrow {CD} $ ta được:
Cho hình vuông ABCD có cạnh bằng a. Tích $\overrightarrow {AB} .\overrightarrow {AC} $ bằng:
Khi nuôi cá thí nghiệm trong hồ, một nhà khoa học đã thấy rằng: Nếu trên mỗi đơn vị diện tích của mặt hồ có x con cá $\left( {x \in {\mathbb{Z}^ + }} \right)$ thì trung bình mỗi con cá sau một vụ cân nặng là $480 - 2x{\mkern 1mu} {\mkern 1mu} \left( {gam} \right)$. Hỏi phải thả bao nhiêu con cá trên một đơn vị diện tích của mặt hồ để sau mỗi vụ thu hoạch được nhiều cá nhất?
Tìm tất cả các giá trị thực của tham số $m$ để bất phương trình $ - 2{x^2} + 2\left( {m - 2} \right)x + m - 2 \ge 0$ có nghiệm.
Tìm $m$ để phương trình $\sqrt {{x^2} + mx + 2} {\rm{\;}} = 2x + 1$ có 2 nghiệm phân biệt.
Vịnh Vân Phong – tỉnh Khánh Hòa nổi tiếng vì có con đường đi bộ xuyên biển nối từ Hòn Quạ đến đảo Điệp Sơn. Một du khách muốn chèo thuyền kayak từ vị trí $C$ trên Hòn Quạ đến vị trí $B$ trên Bè thay vì đi bộ xuyên qua con đường qua vị trí $A$ rồi mới đến vị trí $B$ (coi con đường AC, AB, BC là các đường thẳng). Nếu người đó chèo thuyền với vận tốc không đổi là $4$ km/h thì sẽ mất bao nhiêu thời gian biết $AB = 0,4$ km, $AC = 0,6$ km và góc giữa AB và AC là ${60^0}$?
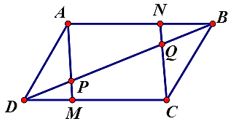
Cho hình bình hành ABCD. Trên các đoạn thẳng$DC,{\mkern 1mu} {\mkern 1mu} AB$ theo thứ tự lấy các điểm $M,{\mkern 1mu} {\mkern 1mu} N$ sao cho $DM = BN$. Gọi $P$ là giao điểm của $AM,{\mkern 1mu} {\mkern 1mu} DB$ và $Q$ là giao điểm của $CN,{\mkern 1mu} {\mkern 1mu} DB$. Khẳng định nào sau đây là đúng?
Cho tam giác ABC đều cạnh a. Điểm M thỏa mãn $\left| {\overrightarrow {MA} {\rm{ \;}} - \overrightarrow {MB} } \right| = \left| {\overrightarrow {MC} } \right|$ là:
Cho tam giác ABC và giả sử $M$ là điểm thỏa mãn đẳng thức $x\overrightarrow {MA} {\rm{\;}} + y\overrightarrow {MB} {\rm{\;}} + z\overrightarrow {MC} {\rm{\;}} = \vec 0$ (trong đó $x,{\mkern 1mu} {\mkern 1mu} y,{\mkern 1mu} {\mkern 1mu} z$ là các số thực). Khẳng định nào sau đây là đúng?
Cho ba điểm $O,{\mkern 1mu} {\mkern 1mu} A,{\mkern 1mu} {\mkern 1mu} B$ không thẳng hàng. Điều kiện cần và đủ để tích vô hướng $\left( {\overrightarrow {OA} {\rm{\;}} + \overrightarrow {OB} } \right).\overrightarrow {AB} {\rm{\;}} = 0$ là
Cho bất phương trình: ${x^2} + mx + {m^2} + 6m < 0$ .Để bất phương trình nghiệm đúng $\forall x \in \left( {1;2} \right)$ thì giá trị nguyên nhỏ nhất của $m$ là:
Cho hình bình hành ABCD có đường chéo lớn là AC. Gọi E,F lần lượt là hình chiếu vuông góc của $C$ trên AB,AD. Biểu thức nào sau đây là đúng?
Tìm tập xác định ${\rm{D}}$ của hàm số $y = \sqrt {6 - 3x} - \sqrt {x - 1} .$
Mệnh đề phủ định của mệnh đề “$\forall x \in \mathbb{R},\,\,x - 2 > 5$” là:
Cho tập hợp $D = \left\{ {x \in {\mathbb{N}^*}|x\left( {x - 2} \right)\left( {x - 3} \right) = 0} \right\}$. Viết lại tập hợp D dưới dạng liệt kê các phần tử của tập hợp đó.
Xét sự biến thiên của hàm số $y = \frac{1}{{{x^2}}}$. Mệnh đề nào sau đây đúng?
Cho hai tập hợp $A = \left( { - \infty ; - 2} \right]$ và $B = \left( { - 3;5} \right]$. Tìm mệnh đề sai.
Trong các tập hợp sau, tập hợp nào là tập con của tập hợp $A = \left\{ {1;2;3;4;5} \right\}$?
Cho parabol $\left( P \right):y = 3{x^2} - 2x + 1$. Điểm nào sau đây là đỉnh của $\left( P \right)$?
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
Điểm nào dưới đây thuộc miền nghiệm của bất phương trình $3x + 2y < 10$?
Trong tam giác EFG, chọn mệnh đề đúng.

.png)
.png)

.png)
.png)
.png)
.png)
.png)
.png)
.png)
