Đề thi thử giữa học kỳ 1 môn Toán lớp 10 online - Mã đề 05
Vui lòng cài đặt đề thi trước khi làm bài
Hãy xác định kết quả của phép toán $\left[ { - 1;9} \right)\backslash \left( { - 7;5} \right]$
Tìm tập xác định của hàm số $y = \sqrt {x + 5} $.
Hàm số nào sau đây là hàm số lẻ?
Hàm số $y = \dfrac{{9x - 1}}{{x + 6}}$ xác định khi nào?
Cho hai tập hợp $A = \left\{ {3;4;5;6} \right\}$ và $B = \left\{ {5;6;7} \right\}$. Kết quả của phép toán $A \cap B$ là
Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng $d:y = 5x - 99$ và $d':y = 5x + 11$. Mệnh đề nào là đúng?
Cho parabol $\left( P \right):y = {x^2} - 4x + 1.$ Tọa độ đỉnh I của parabol $\left( P \right)$ là
Cho tập hợp $A = \left\{ {b;d} \right\}$. Tập hợp $A$ có tất cả bao nhiêu tập con?
Tìm tất cả giá trị của tham số m để hàm số $y = \left( {m - 5} \right)x + 2019$ nghịch biến trên $\mathbb{R}$
Đường thẳng $d:y = x + 3$ cắt parabol $\left( P \right):y = 3{x^2} + 10x + 3$ tại hai điểm có hoành độ lần lượt là
Cho hàm số $y = 2{x^2} - 4x$ có đồ thị như hình vẽ. Có tất cả giá trị nguyên của tham số $m$thuộc đoạn $\left[ {0;5} \right]$ để phương trình $2{x^2} - 4x = 3m$ có hai nghiệm phân biệt?
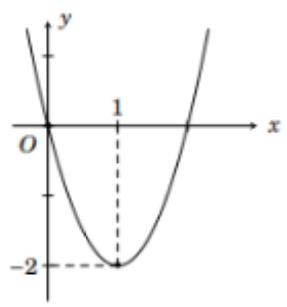
Hàm số nào sau đây có đồ thị như hình vẽ?
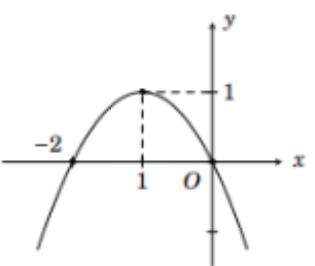
Cho hàm số $y = f\left( x \right)$ có đồ thị trên đoạn $\left[ {1;\,\,5} \right]$ như hình vẽ. Mệnh đề nào sau đây là đúng?
Cho giá trị của tham số m để hai đường thẳng $\Delta :y = \left( {3m - 2} \right)x - 3,\,\,\Delta ':y = 2x - 5$ vuông góc với nhau.
Đồ thị trong hình vẽ là đồ thị của hàm số nào trong các hàm số sau?
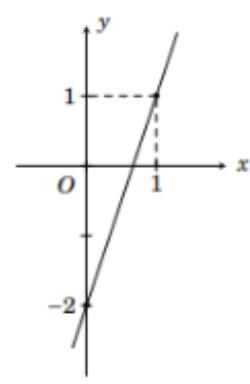
Trong các đẳng thức sau đây, đẳng thức nào sai?
Tam giác ABC có$a = 7,b = 5,\angle C = {60^o}$. Độ dài cạnh c bằng bao nhiêu?
Trong mặt phẳng tọa độ Oxy cho các điểm $A\left( {1; - 2} \right);B\left( { - 3;5} \right)$. Tọa độ điểm M thỏa mãn $2\overrightarrow {MA} - 3\overrightarrow {MB} = \overrightarrow 0 $ là:
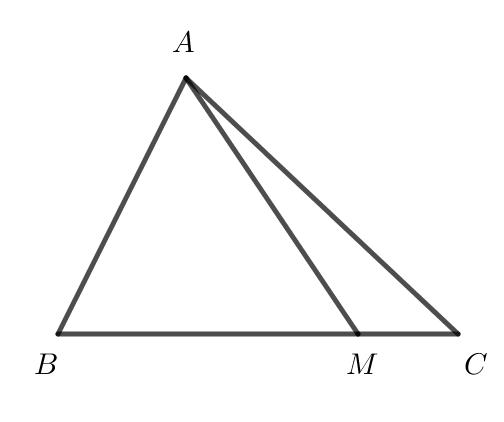
Gọi điểm M là điểm thuộc cạnh BC của tam giác ABC sao cho BM = 3MC . Khi đó $\overrightarrow {AM} $ bằng:
Cho véc tơ$\overrightarrow a = \left( {1; - 2} \right)$. Với giá trị nào của y thì véc tơ $\overrightarrow b = \left( {3;y} \right)$ tạo với véc tơ $\overrightarrow a $ một góc ${45^o}$:
Khi sử dụng máy tính bỏ túi với 10 chữ số thập phân ta được $\sqrt 8 = 2,828427125$. Giá trị gần đúng của $\sqrt 8 $ chính xác đến hàng phần trăm là
Cho mệnh đề A: “$\forall x \in R,{x^2} - x + 7 < 0$”. Mệnh đề phủ định của A là
Cho A ={ 1,2,3}, số tập con của A là
Cho G là trọng tâm $\Delta $ABC, O là điểm bất kỳ thì ta có:
Hãy chọn mệnh đề đúng:
Trong các câu sau, câu nào là mệnh đề chứa biến?
Phủ định của mệnh đề : $\pi $ là số vô tỷ là
Cho $A = \left\{ {x \in \mathbb{R},{\rm{ }}x \ge 3} \right\}$. Trong các tập hợp sau tập nào bằng tập A?
Cho hai tập hợp $M = \{ 1;2;3;5\} ,$$N = \{ 2;6; - 1\} $. Xét các khẳng định sau đây:
$\begin{array}{l}M \cap N = \{ 2\} \\N\backslash M = \{ 1;3;5\} \\M \cup N = \{ 1;2;3;5;6; - 1\} \end{array}$
Có bao nhiêu khẳng định đúng trong ba khẳng định nêu trên?
Cho tam giác ABC có G là trọng tâm, M là trung điểm của BC, đẳng thức nào sau đây là đúng ?
Cho $\Delta ABC$ với M là trung điểm của BC, đẳng thức nào sau đây là đúng ?
Cho $A = \left\{ {n \in \mathbb{N}:n < 5} \right\}$, tập A là tập hợp nào trong các tập sau?
Phát biểu nào sau đây không phải là mệnh đề ?
Cho $A = \left\{ {0;2;4;6} \right\}$. Tập A có bao nhiêu phần tử?
Cho 4 điểm A, B, C, D bất kỳ, chọn đẳng thức đúng:
Cho tập hợp $X = \{ x \in \mathbb{R}|x - 1 > 0\} .$ Hãy chọn khẳng định đúng.
Cho số gần đúng a = 2 841 275 với độ chính xác d = 300. Số quy tròn của số a là
Số phần tử của tập hợp A = $\left\{ {{k^2} + 1|k \in \mathbb{Z},{\rm{ }}\left| k \right| \le 2} \right\}$ là
Xác định vị trí 3 điểm A, B, C thỏa hệ thức: $\overrightarrow {AB} = \overrightarrow {CA} $ là:
Cho hình chữ nhật ABCD, đẳng thức nào sau đây là đúng ?

.jpg)
.PNG)