Thi thử trắc nghiệm ôn tập môn Quản lý dự án đầu tư online - Đề #11
Vui lòng cài đặt đề thi trước khi làm bài
Công thức: ${t_{ei}} = ({t_0} + 4{t_m} + {t_p})/6$ dùng để xác định:
Chọn đáp án đúng. Công thức sau đây: ${t_{ei}} = (2{t_0} + 3{t_p})/5$ dùng để xác định:
Tìm đáp án đúng dưới đây. Công thức ${T_p} = \sum\limits_{i = 1}^n {{t_{ei}}} $ dùng để tính:
Công việc X có thời gian bi quan là 15 ngày, thời gian lạc quan là 9 ngày, thời gian thường gặp là 12 ngày. Vây thời gian thực hiện dự tính của công việc X là:
Công việc Y có thời gian bi quan là 9 tuần, thời gian lạc quan là 5 tuần, thời gian thường gặp là 7 tuần. Vậy thời gian thực hiện dự tính của công việc Y trong trường hợp này so với trường hợp không xác định được thời gian thường gặp, ngắn hơn:
Dự án có sơ đồ PERT như sau:
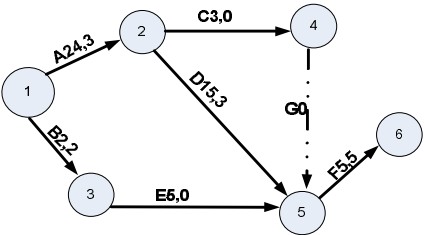
Vậy thì thời gian thực hiện dự tính của dự án là:
Dự án có sơ đồ PERT dưới đây. Vậy thì đường găng của dự án là:
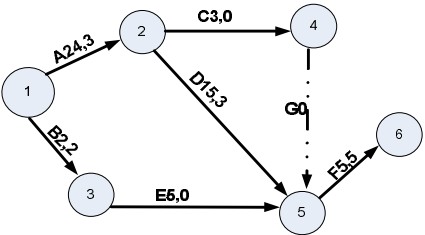
Dự án có sơ đồ PERT như sau:
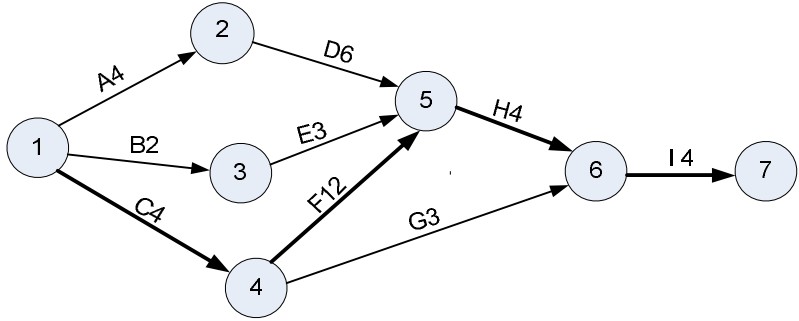
Tiến trình tới hạn trên sơ đồ này là:
Dự án có sơ đồ PERT như sau: 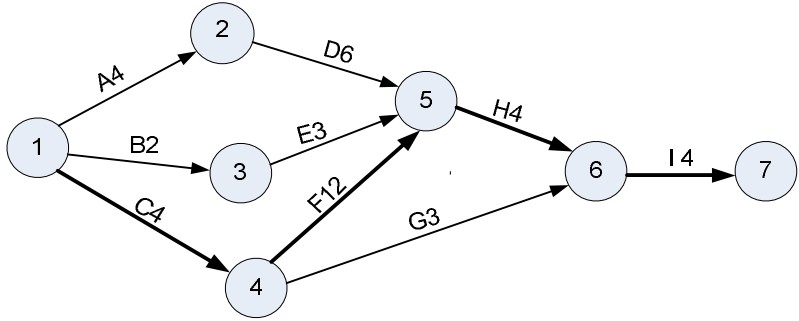
Vậy tổng thời gian (tính theo tháng) thực hiện dự án này là:
Dự án có sơ đồ PERT như sau:
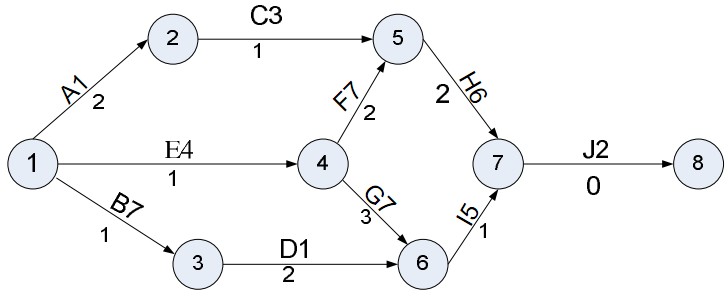
Vậy dự án này có:
Cho dự án có sơ đồ PERT như sau:
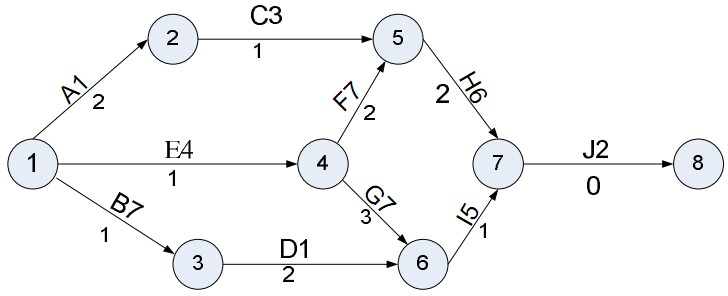
Vậy tiến trình tới hạn của dự án này là:
Dự án có sơ đồ PERT như sau:

Vậy thời gian (tuần) hoàn thành dự án này là:
Dự án có sơ đồ PERT như sau:
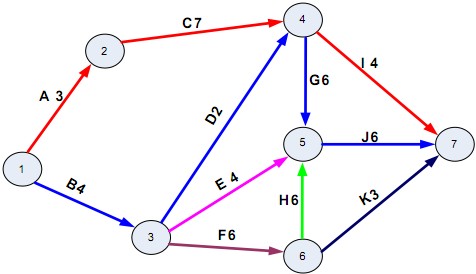
Dự án này có:
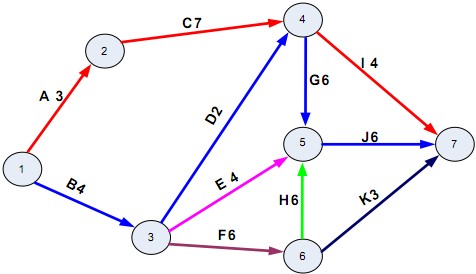
Dự án có sơ đồ PERT như sau:

Số đường găng của sơ đồ PERT là:
Dự án có sơ đồ PERT dưới đây. Thời gian (tuần) hoàn thành dự án này là:
Chọn đáp án đúng đưới đây. Công thức dưới đây: $S_p^2 = \sum\limits_{i = 1}^n {{S^2}ei}$ dùng để tính:
Trong công thức: ${S_{ei}} = \sqrt {{S^2}_{ei}} $ thì:
Căn cứ vào công thức dưới đây để chọn đáp án sai trong số 4 đáp án:
${T_p} = \sum\limits_{i = 1}^n {{t_{ei}}} $
Chọn đáp án đúng dưới đây: Công thức: ${\left( {\frac{{{t_p} - {t_0}}}{6}} \right)^2}$ dùng để tính:
Công thức: $\left( {\frac{{{t_p} - {t_0}}}{6}} \right)$ dùng để tính:
Cho biết thời gian bi quan để thực hiện một công việc là 20 ngày, thời gian lạc quan là 15 ngày. Vậy độ lệch chuẩn về thời gian của công việc này là:
Cho biết thời gian bi quan để thực hiện một công việc là 20 ngày, thời gian lạc quan là 10 ngày. Vậy phương sai về thời gian của công việc này là:
Một tiến trình của dự án có ba công việc : A, B và C. A, B là các công việc thực, C là công việc ảo. Cho biết: Phương sai của công việc A là 1,25 ; của công việc B là 1,35. Vậy phương sai của cả tiến trình là:
Đường găng của một dự án chỉ có 2 công việc là X và Y. Phương sai của công việc X là 1,8; phương sai của công việc Y là 1,2. Vậy độ lệch chuẩn về thời gian của đường găng là:
Câu nào sai trong các câu câu dưới đây?
Cho sơ đồ PERT của một dự án, trong đó số viết sau tên công việc là thời gian thực hiện dự tính của công việc đó.
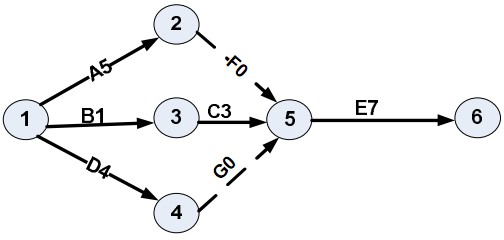
Và biết thêm: Thời gian lạc quan để thực hiện công việc A là 3 tuần, thời gian bi quan là 8 tuần. Vậy thời gian thường gặp khi thực hiện công việc A, là:
Cho sơ đồ PERT của một dự án, trong đó số viết sau tên công việc là thời gian thực hiện dự tính của công việc đó. Và biết thêm: Thời gian lạc quan để thực hiện công việc C là 2 tuần, thời gian thường gặp là 3 tuần. Vậy thời gian bi quan khi thực hiện công việc C, là:
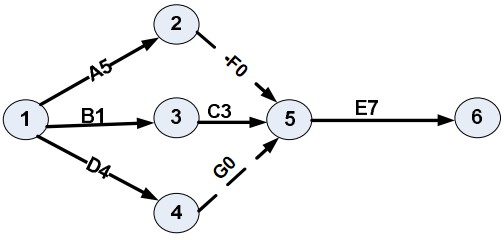
Cho sơ đồ PERT của một dự án, trong đó số viết sau tên công việc là thời gian thực hiện dự tính của công việc đó. Và biết thêm: Thời gian bi quan để thực hiện công việc E là 10 tuần, thời gian thường gặp là 6,75 tuần. Vậy thời gian lạc quan khi thực hiện công việc E, là:
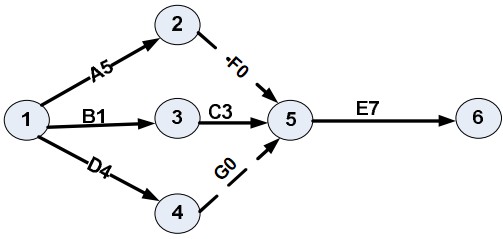
Dự án lắp ghép một khu nhà công nghiệp, có các công việc:
(A) Làm móng nhà, thời gian thực hiện dự tính 5 tuần, bắt đầu ngay.
(B) Vận chuyển cần cẩu về, 1 tuần, bắt đầu ngay.
(C) Lắp dựng cần trục, 3 tuần, sau vận chuyển cần cẩu.
(D) Vận chuyển cấu kiện, 4 tuần, bắt đầu ngay.
(E) Lắp ghép khung nhà và lợp mái, 7 tuần, sau lắp cần cẩu”
Căn cứ vào quy trình công nghệ, người ta đã vẽ sơ đồ GANTT như sau:

Quy trình tính xác suất hoàn thành dự án, có:

